The proposed 10 band graphic equalizer circuit can be used in conjunction with any existing audio amplifier system to get an enhanced 10 stage audio processing, and customized tone control.
The circuit can be easily converted to a 5 band graphic equalizer by simply eliminating 5 stages from the shown design
The Circuit Concept
A graphic equalizer is a type of complex tone control circuit which can be applied to smooth out or enhance the frequency response of any hi-fi audio amplifier, or in a guitar effects unit. To be precise, the unit can prove effective in virtually any form of audio application.
The unit is quite simple to use. All one has to do is feed the TV or PC audio input to this circuit and hook the output with the existing home theater amplifier.
Next, it would be just a matter of adjusting the given 10 band controls and enjoying the vastly improved sound quality.
You would be able to tailor the sound as per your preferred tastes.As an example, the midrange controls of the equalizer can be adjusted to highlight dialogue or in order to reduce the harshness over a particular range of voice audio.
Or perhaps you can roll off the high pitched even to further extents in case you wished, or simply heightened the bas boost to your liking.
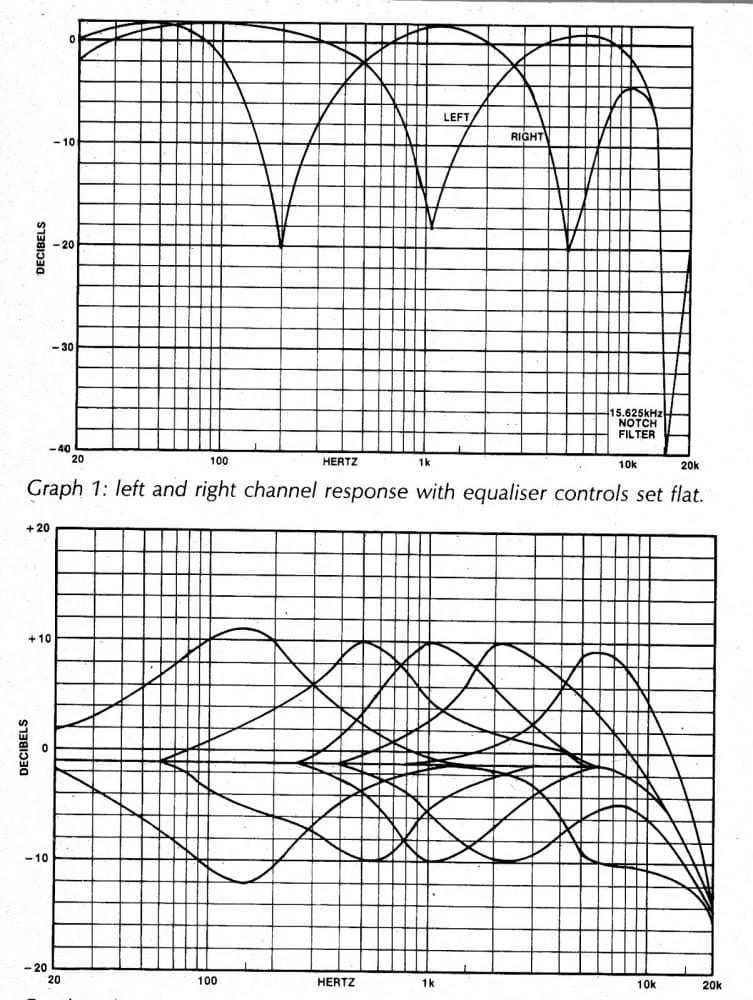
Typically the controls would be able to provide upto 10dB of boost or cut at nominal center frequencies of 150Hz, 500Hz, 1kHz, 2kHz, 5kHz, 7kHz, 10kHz, 13kHz, 15kHz, 18kHz.
The circuit also includes a fixed 10kHz low pass filter stage for cancelling out unwanted noise such as hiss or other high frequencies disturbances.
How the 10 band graphic equalizer circuit functions
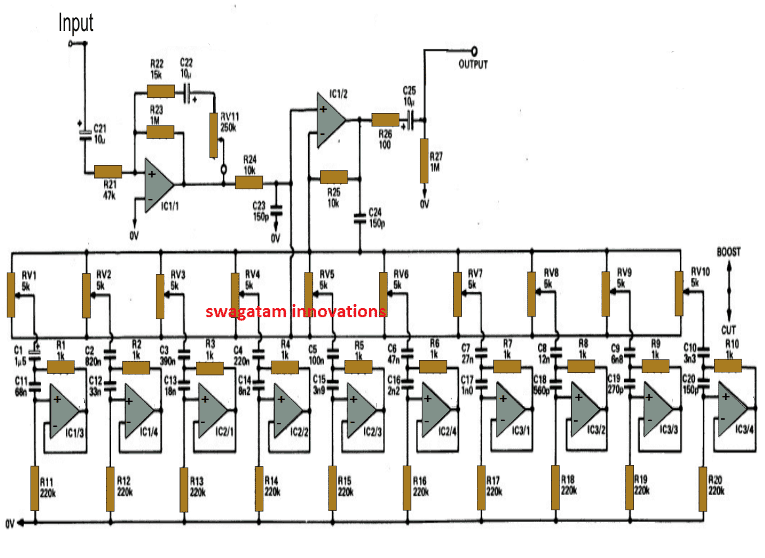
Referring to the given circuit diagram we can see that the associated opamps form the main active component responsible for the required optimizations.
You will notice that all the 10 stages are identical, it's the difference in the values of the incuded capacitors and the pot which effectively varies the processing leves across the various stages.
For analyzing the operation we may consider any one of the opamp stages since all of them are identical.
Here the opamps act as "gyrators" which refers to an opamp circuit which effectively converts a capacitive response to an inductance response.
Consider an AC voltage source Vi connected to the opamp stage. This pushes a current Ic via the capacitor (C1, C2, C3 etc), which constitutes a proportional voltage across the connected ground resistance (R11, R12, R13 etc).
This voltage across the ground resistance is conveyed at the ouput of the opamp.
Due to this the voltage across the feedback resistor (R1, R2, R3 etc) becomes equal to the difference between Vin and Vout which causes current to flow via the feedback resistor and back into the input voltage source!
A careful assessment of the phases of the above developed current would show that as Ic leads the voltage Vin (as it can expected for any capacitive circuit) the net input current that may be the vector sum of Ic and Io in fact trails the voltage Vi.
Using Capacitors as Tuned Inductors
Therefore this implies that in effect, the capacitor C has gotten transformed into a virtual inductor due to the actions of the opamp.
This transformed "inductance" may be expressed by the following equation:
L = R1xR2xC
where R1 = ground resistance, R2 = feedback resistance while C = capacitor at the non-inverting input of the op amp.
Here C would be in Farads and the resistances in Ohms.
The pots effectively vary the input current to the opamps which results in a change in the value of the above explained "inductance", which in turn results in the required music enhancement in the form of treble cuts or bass boosts.
Circuit Diagram
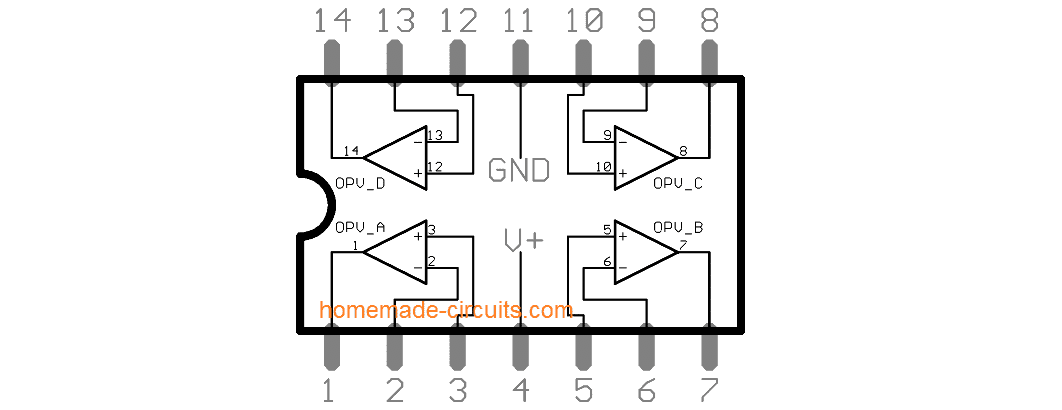
LM324 IC Pinout Details
Parts List
- All resistor are 1/4 watt 1%
- R1----R10 = 1K
- R11---R20 = 220k
- R21 = 47K
- R22 = 15K
- R23, R27 = 1M
- R24, R25 = 10K
- R26 = 100 ohm
- RV1----RV10 = 5K pot
- RV11 = 250K pot
- All pF and nF capacitors are metallized polyester 50V
- C1 = 1.5uF
- C2 = 820nF
- C3 = 390nF
- C4 = 220nF
- C5 = 100nF
- C6 = 47nF
- C7 = 27nF
- C8 = 12nF
- C9 = 6.8nF
- C10 = 3n3
- C11 = 68nF
- C12 = 33nF
- C13 = 18nF
- C14 = 8.2nF
- C15 = 3.9nF
- C16 = 2.2nF
- C17 = 1nF
- C18 = 560pF
- C90 = 270pF
- C20 = 150pF
- C21, C22, C25 = 10uF/25V
- C23, C24 = 150pF
- Op amps = 4nos LM324
Response Curve for the above 10 band graphic equalizer design
Simplified Version
The simplified version of the above explained graphic equalizer can be witnessed in the following image:
Parts List
RESISTORS all 1/4W, 5%
R1, R2 = 47k
R3, R4 = 18k
R5, R6 = 1M
R7 = 47k
R8, R9 =18k
R10, R11 = 1M
R12 = 47k
R13, R14 = 18k
R15, R16 = 1M
R17 = 47k
R18, R19 = 18k
R20, R21 = 1M
R22, R23 = 47k
R24, R25 = 4k7
POTENTIOMETERS
RV1 10k log slider pot
RV2, 3, 4, 5 … . 100k linear slider pot
CAPACITORS
C1 = 220n PPC
C2 = 470p PPC
C3 = 47p ceramic
C4 = 2n2 PPC
C5 = 220p ceramic
C6 = 8n2 PPC
C7 = 820p ceramic
C8 = 33n PPC
C9 = 3n3 PPC
C10, C11 = 100µ 25V electrolytic
SEMICONDUCTORS
IC1-1C6 = 741 op amp
D1 = IN914 or 1N4148
MISCELLANEOUS
SW1 spst miniature toggle switch
SKI, 2 mono jack sockets
B1, 2 9V 216 batteries
5 Band Active Equalizer Circuit
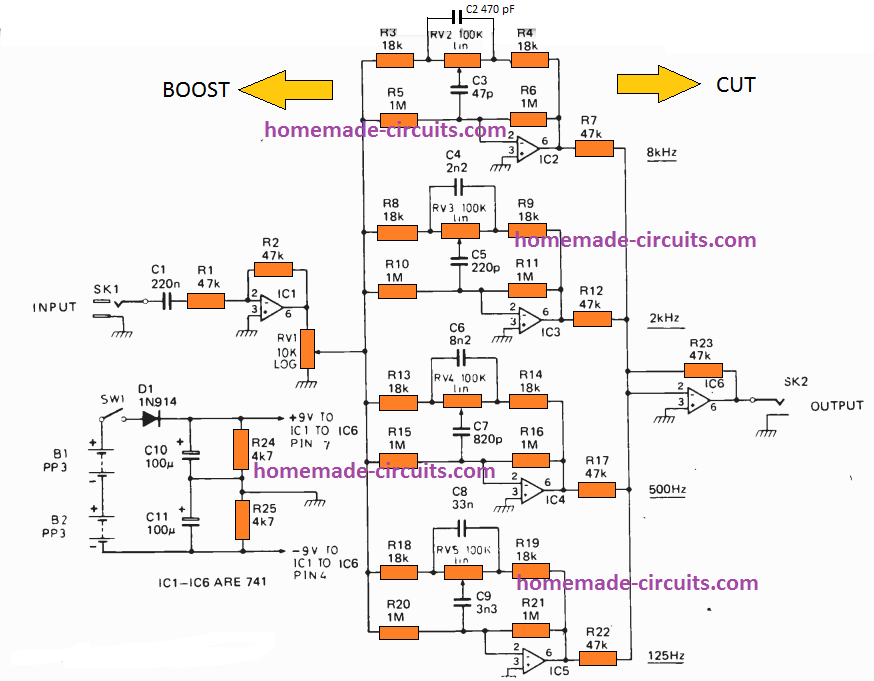
According to the circuit architecture shown below, the input signal is capacitively linked to the non-inverting input of IC1a, which is used to buffer the signal since at this point a low impedance is needed to reduce noise pickup on the potentiometer wires.
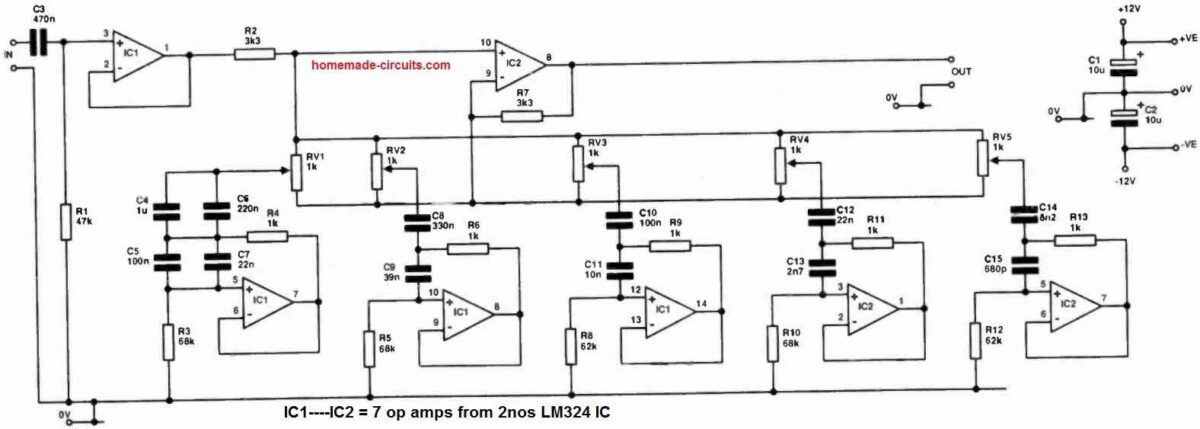
For now, let's ignore the potentiometers. The signal is sent through R2 to IC2c, which acts as a unity-gain buffer DC-coupled to the output.
If every potentiometer is set to its middle position, any loading on the sliders will pot down the input signal to the non-inverting input of IC2c, while also pot down the negative feedback and producing a gain that compensates for the potting -down of the input signal.
Consequently, we still have unity gain at all frequencies in this situation.
The system displays a net gain at 206 Hz if the slider RV2 is pushed to the inverting input end of its range.
This is because the effect of potting down the negative feedback is, at resonance, considerably stronger than the potting -down of the input signal.
The input signal is potted down but the negative feedback is not, therefore there is a decrease in the frequency response at 206 Hz when the slider turned to the non-inverting input end of its journey.
Each and every potentiometer follows the same logic.
In order to reduce the impacts of crosstalk through the power supply, local decoupling is offered on the board.
Parts List

5 Band Passive Equalizer Circuit
A very neat and reasonably efficient 5 band graphic equalizer circuit using only passive components can e built as shown in the following diagram:
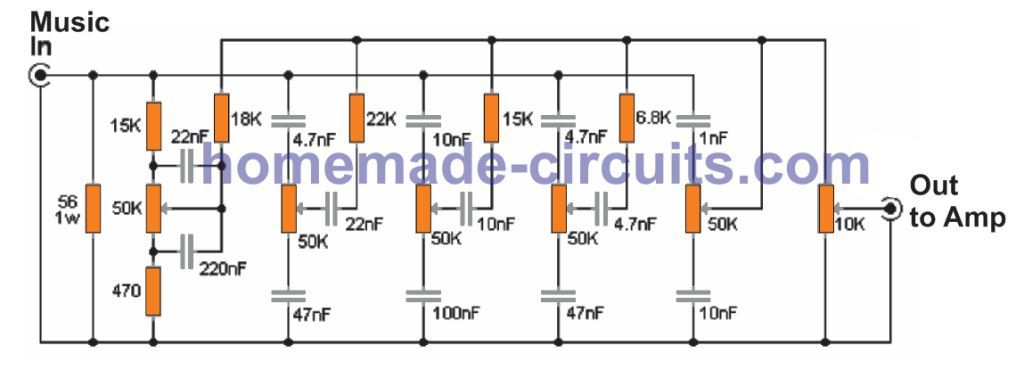
As can be seen in the figure above, the 5 band equalizer has five potentiometers for controlling the tone of the input music signal, while the sixth potentiometer is positioned for controlling the volume of the sound output.
Basically, the shown stages are simple RC filters, which narrow or broaden the frequency passage of the input signal, so that only a certain band of frequency is allowed to pass, depending on the adjustment of the relevant pots.
The equalized frequency bands are 60Hz, 240Hz, 1KHz, 4KHz and 16KHz, from left towards right. Lastly followed by the volume control pot control.
Since the design does not use active components this equalizer is able to operate without any supply input. Please note that if this 5 band equalizer is implemented for a stereo or multichannel system, it may become necessary to set up an equalizer in the identical manner for each of the channels.
Parametric Equalizer Circuit for Enhanced Effect
If you are not impressed with the above 10 band graphic equalizer results, then the following simple parametric equalizer circuit will surely make you feel a lot happier.
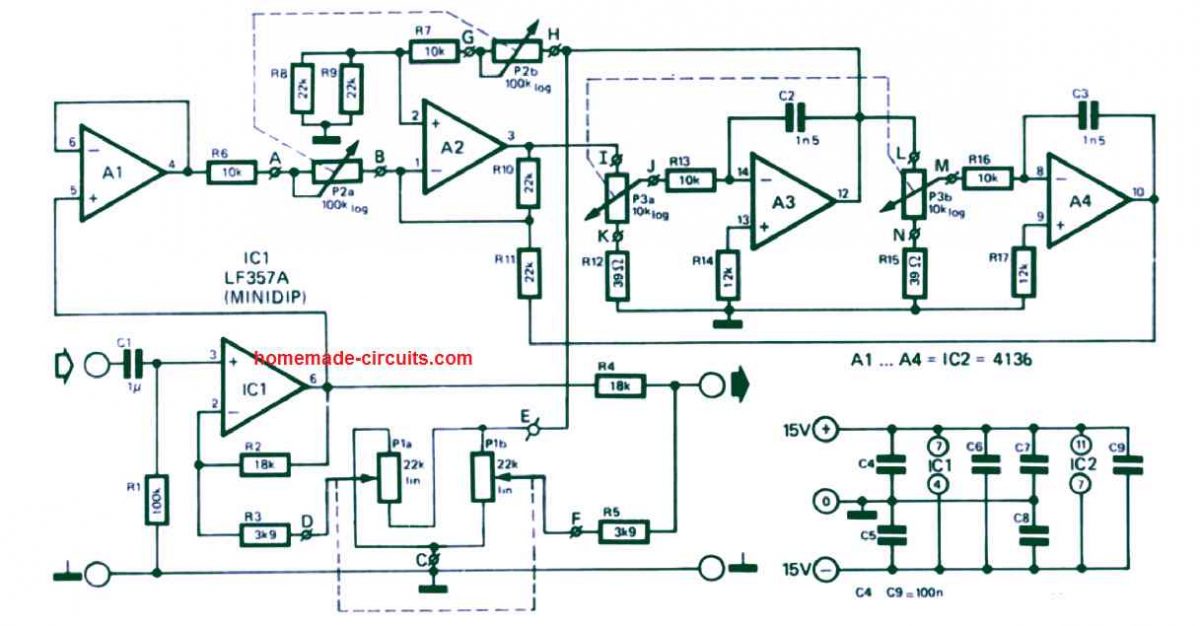
Audio input is sent from left side at the input of C1, while the enhanced equalizer effect is acquired from the right side R4 end which must be connected to the power amplifier.
The dotted lines indicate that the relevant potentiometers must be dual type pots, and must move concurrently.
The effect from such parametric equalizers or filter circuit is said to be similar to the effects that we normally get in concert halls, and auditoriums.