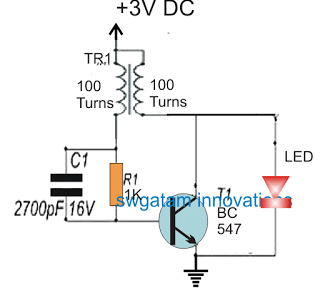
A blocking oscillator is one of the simplest form of oscillators which is able to produce self sustaining oscillations through the use of just a few passive and a single active component.
The name "blocking" is applied due to fact that the switching of the main device in the form of a BJT is blocked (cut-of) more often than it's allowed to conduct during the course of the oscillations, and hence the name blocking oscillator.
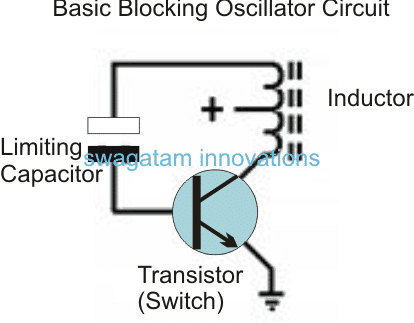
Where a Blocking Oscillator is Typically Used
This oscillator will generate a square wave output which can be effectively applied for making SMPS circuits or any similar switching circuits, but cannot be used for operating sensitive electronic equipment.
The tone notes generated with this oscillator become perfectly suitable for alarms, morse code practice devices, wireless battery chargers etc. The circuit also becomes applicable as strobe light in cameras, which can be often seen just before clicking the flash, this feature helps in reducing the infamous red eye effect.
Due to its simple configuration, this oscillator circuit is widely used in experimental kits, and the students find it much easier and interesting to grasp it details quickly.
How a Blocking Oscillator Works
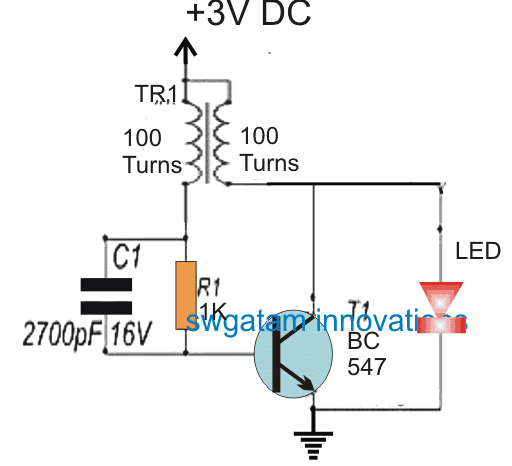
For making a blocking oscillator, the selection of the components become quite critical so that it is able to work with optimal effects.
The concept of a blocking oscillator is actually very flexible, and the outcome from it can be extensively varied, simply by varying the characteristics of the involved components such as the resistors, the transformer.
The transformer here specifically becomes a crucial part and the output waveform heavily depends on the type or the make of this transformer. For example when a pulse transformer is used in a blocking oscillator circuit, the waveform attains the shape of rectangular waves consisting of rapid rise and fall periods.
The oscillating output from this design become effectively compatible with lamps, loudspeakers, and even relays.
A single resistor can be seen controlling the frequency of a blocking oscillator, and therefore if this resistor is replaced with a pot, the frequency becomes manually variable and can be tweaked as per the users requirement.
However care should be taken not to reduce the value below a specified limit which could otherwise damage the transistor and create unusually unstable output waveform characteristics. It is always recommended to position a safe minimum value fixed resistor in series with the pot to prevent this situation.
Circuit operation
The circuit works with the help of positive feedbacks across the transformer by associating two switching time periods viz, the time Tclosed when the switch or the transistor is closed, and the time Topen when the transistor is open (not conducting). The following abbreviations are used in the analysis:
- t, time, one of the variables
- Tclosed: instant at the end of the closed cycle, initialization of the open cycle. Also a magnitude of the time duration when the switch is closed.
- Topen: instant at the every end of the open cycle, or the beginning of closed cycle. Same as T=0. Also a magnitude of the time duration whenever the switch is open.
- Vb, supply voltage e.g. Vbattery
- Vp, voltage within the primary winding. An ideal switching transistor will allow a supply voltage Vb across the primary, therefore in an ideal situation Vp will be = Vb.
- Vs, voltage across the secondary winding
- Vz, fixed load voltage resulting due to for e.g. by the opposite voltage of a Zener diode or the forward voltage of a connected (LED).
- Im, magnetizing current across the primary
- Ipeak,m, highest or the "peak" magnetizing current on the primary side of the trafo. Takes place just before Topen.
- Np, the number of primary turns
- Ns, the number of secondary turns
- N, the ratio of winding also defined as Ns/Np, . For an perfectly configured transformer working with ideal conditions, we have Is = Ip/N, Vs = N×Vp.
- Lp, primary self-inductance, a value calculated by the number of primary turns Np squared, and an "inductance factor" AL. Self-inductance is frequently expressed with the formula Lp = AL×Np2×10−9 henries.
- R, combined switch (transistor) and the primary resistance
- Up, energy accumulated within the flux of the magnetic field across the windings, as expressed by the magnetizing current Im.
Operation during Tclosed (time when the switch is closed)
The moment the switching transistor activates or triggers it applies the source voltage Vb over the transformer primary winding.
The action generates a magnetizing current Im on the transformer as Im = Vprimary×t/Lp;
where t (time) may be a changing with time and initiates at 0. The specified magnetizing current Im now "rides upon" any reverse generated secondary current Is which may happen to induce into the load on the secondary winding (for instance into the control terminal (base) of the switch (transistor) and subsequently reverted to secondary current in primary = Is/N).
This altering current at the primary in turn generates an altering magnetic flux within the transformer's windings; which enables quite a stabilized voltage Vs = N×Vb across the secondary winding.
In many of the configurations the secondary side voltage Vs may add up with the supply voltage Vb; due to the fact that the voltage on the primary side is approximately Vb, Vs = (N+1)×Vb while the switch (transistor) is in the conducting mode.
Thus, the switching procedure may have the tendency to acquire a portion of its control voltage or current directly from Vb while the remaining through Vs.
This implies that the switch-control voltage or the current would be "in phase"
However in a situation of an absence of a primary resistance and negligible resistance on the transistor switching, might result in a rise in the magnetizing current Im with a "linear ramp" which may be expressed by the formula as given first paragraph.
Conversely suppose there is a significant magnitude of primary resistance for the transistor or both (combined resistance R, e.g. primary-coil resistance along with a resistor attached with the emitter, FET channel resistance), then the Lp/R time constant could result in a rising magnetizing current curve with consistently dropping slope.
In both the scenarios the magnetizing current Im will have a commanding effect through the combined primary and the transistor current Ip.
This also implies that if a limiting resistor is not included the effect could increase infinitely.
However, as studied above during the first case (low resistance), the transistor might ultimately fail to handle the excess current, or simply put, its resistance might tend to rise to an extent where the voltage drop across the device might become equal to the supply voltage; causing complete saturation of the device (which may be evaluated from a transistor's gain hfe or "beta" specs).
In the second situation (e.g. inclusion of a significant primary and/or emitter resistance) the (dropping) slope of the current might reach a point where the induced voltage over the secondary winding is simply not sufficient to keep the transistor in the conducting position.
In the third scenario, the core used for the transformer might reach the saturation point and collapse which int turn would stop it from supporting any further magnetization, and prohibit the primary to secondary induction process.
Thus, we can conclude that during all the three situations as discussed above, the rate at which the primary current rises or the rate of rise of the flux in the core of the trafo in the third case, might show a dropping tendency towards zero.
Having said this, in the first two scenarios, we find that despite of the fact the primary current seems to continue its supply, its value touches a constant level which might be just equal to the supply value given by Vb divided by the sum of the resistances R at the primary side.
In such a "current-limited" condition the transformer's flux might tend to show a steady state. Except the changing flux, which might keep inducing voltage across the secondary side of the trafo, this implies that a steady flux is indicative towards a failure of induction process across the winding resulting in the secondary voltage dropping to zero. This causes the switch (transistor) to open.
The above comprehensive explanation clearly explains how a blocking oscillator works and how this highly versatile and flexible oscillator circuit may be used for any specified application and fine tuned to the desired level, as the user may prefer to implement.