Calculating ferrite transformer is a process in which engineers evaluate the various winding specifications, and core dimension of the transformer, using ferrite as the core material. This helps them to create a perfectly optimized transformer for a given application.
The post presents a detailed explanation regarding how to calculate and design customized ferrite core transformers. The content is easy to understand, and can be very handy for engineers engaged in the field of power electronics, and manufacturing SMPS inverters.

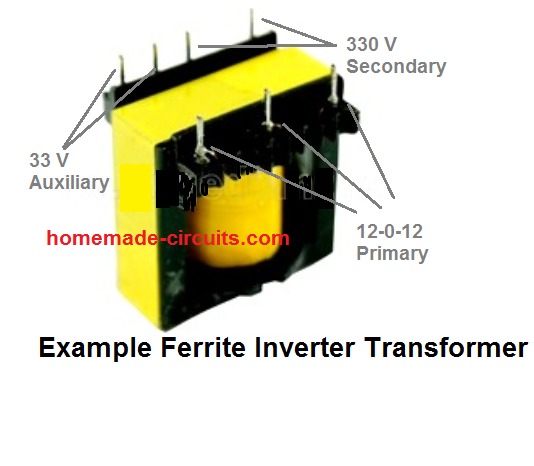
Why Ferrite Core is used in High Frequency Converters
You might have often wondered the reason behind using ferrite cores in all modern switch mode power supplies or SMPS converters. Right, it is to achieve higher efficiency and compactness compared to iron core power supplies, but it would be interesting to know how ferrite cores allow us to achieve this high degree of efficiency and compactness?
It is because in iron core transformers, the iron material has much inferior magnetic permeability than ferrite material. In contrast, ferrite cores possess very high magnetic permeability.
Meaning, when subjected to a magnetic field, ferrite material is able to achieve a very high degree of magnetization, better than all other forms of magnetic material.
A higher magnetic permeability means, lower amount of eddy current and lower switching losses. A magnetic material normally has a tendency to generate eddy current in response to a rising magnetic frequency.
As the frequency is increased, eddy current also increases causing heating of the material and increase in coil impedance, which leads to further switching losses.
Ferrite cores, due to to their high magnetic permeability are able to work more efficiently with higher frequencies, due to lower eddy currents and lower switching losses.
Now you may think, why not use lower frequency as that would conversely help to reduce eddy currents? It appears valid, however, lower frequency would also mean increasing the number of turns for the same transformer.
Since higher frequencies allow proportionately lower number of turns, results in transformer being smaller, lighter and cheaper. This is why SMPS uses a high frequency.
Inverter Topology
In switch mode inverters, normally two types of topology exits: push-pull, and Full bridge. The push pull employs a center tap for the primary winding, while the full bridge consists a single winding for both primary and secondary.
Actually, both the topology are push-pull in nature. In both the forms the winding is applied with a continuously switching reverse-forward alternating current by the MOSFETs, oscillating at the specified high frequency, imitating a push-pull action.
The only fundamental difference between the two is, the primary side of the center tap transformer has 2 times more number of turns than the Full bridge transformer.
How to Calculate Ferrite Core Inverter Transformer
Calculating a ferrite core transformer is actually quite simple, if you have all the specified parameters in hand.
For simplicity, we'll try to solve the formula through an example set up, let's say for a 250 watt transformer.
The power source will be a 12 V battery. The frequency for switching the transformer will be 50 kHz, a typical figure in most SMPS inverters. We'll assume the output to be 310 V, which is normally the peak value of a 220V RMS.
Here,the 310 V will be after rectification through a fast recovery bridge rectifier, and LC filters. We select the core as ETD39.
As we all know, when a 12 V battery is used, it's voltage is never constant. At full charge the value is around 13 V, which keeps dropping as the inverter load consumes power, until finally the battery discharges to its lowest limit, which is typically 10.5 V. So for our calculations we will consider 10.5 V as the supply value for Vin(min) .
Calculating the Primary Turns
The standard formula for calculating the primary number of turns is given below:
N(prim) = Vin(nom) x 108 / 4 x f x Bmax x Ac Here N(prim) refers to the primary turn numbers. Since we have selected a center tap push pull topology in our example, the result obtained will be one-half of the total number of turns required.
- Vin(nom) = Average Input Voltage. Since our average battery voltage is 12V, let's, take Vin(nom) = 12.
- f = 50 kHz, or 50,000 Hz. It is the preferred switching frequency, as selected by us.
- Bmax = Maximum flux density in Gauss. In this example, we'll assume Bmax to be in the range of 1300G to 2000G. This is the standard value most ferrite based transformer cores. In this example, let’s settle at 1500G. So we have Bmax = 1500. Higher values of Bmax is not recommended as this may result in the transformer reaching saturation point. Conversely, lower values of Bmax may result in the core being underutilized.
- Ac = Effective Cross-Sectional Area in cm2. This information can be collected from the datasheets of the ferrite cores. You may also find Ac being presented as Ae. For the selected core number ETD39, the effective cross-sectional area furnished in the datasheet sheet is 125mm2. That is equal to 1.25cm2. Therefore we have, Ac = 1.25 for ETD39.
The above figures give us the values for all the parameters required for calcuating the primary turns of our SMPS inverter transformer. Therefore, substituting the respective values in the above formula, we get:
N(prim) = Vin(nom) x 108 / 4 x f x Bmax x AcN(prim) = 12 x 108 / 4 x 50000 x 1500 x 1.2 N(prim) = 3.2Since 3.2 is a fractional value and can be difficult to implement practically, we'll round it off to 3 turns. However, before finalizing this value, we have to investigate whether or not the value of Bmax is still compatible and within the acceptable range for this new rounded off value 3.
Because, decreasing the number of turns will cause a proportionate increase in the Bmax, therefore it becomes imperative to check if the increased Bmax is still within acceptable range for our 3 primary turns.
Counter checking Bmax by substituting the following existing values we get:
Vin(nom) = 12, f = 50000, Npri = 3, Ac = 1.25Bmax = Vin(nom) x 108 / 4 x f x N(prim) x Ac Bmax = 12 x 108 / 4 x 50000 x 3 x 1.25 Bmax = 1600As can be seen the new Bmax value for N(pri) = 3 turns looks fine and is well within the acceptable range. This also implies that, if anytime you feel like manipulating the number of N(prim) turns, you must make sure it complies with the corresponding new Bmax value.
Oppositely, it may be possible to first determine the Bmax for a desired number of primary turns and then adjust the number of turns to this value by suitably modifying the other variables in the formula.
Calculating the Secondary Turns
Now we know how to calculate the primary side of an ferrite SMPS inverter transformer, it's time to look into the other side, that is the secondary of the transformer.
Since the peak value has to be 310 V for the secondary, we would want the value to sustain for the entire battery voltage range starting from 13 V to 10.5 V.
No doubt we will have to employ a feedback system for maintaining a constant output voltage level, for countering low battery voltage or rising load current variations.
But for this there has to be some upper margin or headroom for facilitating this automatic control. A +20 V margin looks good enough, therefore we select the maximum output peak voltage as 310 + 20 = 330 V.
This also means that the transformer must be designed such that it can produce 310 V even at the lowest 10.5 battery voltage.
For feedback control we normally employ a self adjusting PWM circuit, which widens the pulse width during low battery or high load, and narrows it proportionately during no load or optimal battery conditions.
This means, at low battery conditions the PWM must auto adjust to maximum duty cycle, for maintaining the stipulated 310 V output. This maximum PWM can be assumed to be 98% of the total duty cycle.
The 2% gap is left for the dead time. Dead time is the zero voltage gap between each half cycle frequency, during which the MOSFETs or the specific power devices remain completely shut off.
This ensures guaranteed safety and prevents shoot through across the MOSFETs during the transition periods of the push pull cycles.
Hence, input supply will be minimum when the battery voltage reaches at its minimum level, that is when Vin = Vin(min) = 10.5 V. This will prompt the duty cycle to be at its maximum 98%.
The above data can be used for calculating the average voltage (DC RMS) required for the primary side of the transformer to generate 310 V at the secondary, when battery is at the minimum 10.5 V. For this we multiply 98% with 10.5, as shown below:
0.98 x 10.5 V = 10.29 V, this the voltage rating our transformer primary is supposed to have.
Now, we know the maximum secondary voltage which is 330 V, and we also know the primary voltage which is 10.29 V.
The turns ratio (n) can be calculated as:
n = Vs / VpSubstituting the given values:
n = 330 / 10.29 ≈ 32.1Since the turns ratio is equal to the voltage ratio, the number of turns on the secondary (Ns) and primary (Np) sides must maintain the same ratio.
This relationship is expressed as:
Ns / Np = nConsidering the primary side has 3 turns (Np = 3), we can solve for Ns:
Ns = n * NpSubstituting the values we get:
Ns = 32.1 * 3 = 96.3Therefore we get the number of secondary turns to be approximately 96.3.
The figure 96.3 is the number of secondary turns that we need for the proposed ferrite inverter transformer that we are designing. As stated earlier since fractional vales are difficult to implement practically, we round it off to 96 turns.
This concludes our calculations and I hope all the readers here must have realized how to simply calculate a ferrite transformer for a specific SMPS inverter circuit.
Calculating Auxiliary Winding
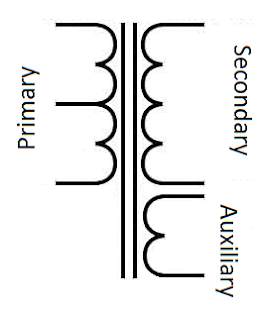
An auxiliary winding is a supplemental winding that a user may require for some external implementation.
Let's say, along with the 330 V at the secondary, you need another winding for getting 33 V for an LED lamp. We first calculate the secondary : auxiliary turn ratio with respect to the secondary winding 310 V rating. The formula is:
NA = Vsec / (Vaux + Vd) NA = secondary : auxiliary ratio, Vsec = Secondary regulated rectified voltage, Vaux = auxiliary voltage, Vd = Diode forward drop value for the rectifier diode. Since we need a high speed diode here we will use a schottky rectifier with a Vd = 0.5V
Solving it gives us:
NA = 310 / (33 + 0.5) = 9.25, let's round it off to 9.Now let's derive the number of turns required for the auxiliary winding, we get this by applying the formula:
Naux = Nsec / NA Where Naux = auxiliary turns, Nsec = secondary turns, NA = auxiliary ratio.
From our previous results we have Nsec = 96, and NA = 9, substituting these in the above formula we get:
Naux = 96 / 9 = 10.66, round it off gives us 11 turns. So for getting 33 V we will need 11 turns on the secondary side.
So in this way you can dimension an auxiliary winding as per your own preference.
Calculating the Wire Thickness
We can calculate the wire thickness by taking into account the current flowing through the primary and secondary windings.
The formula for current is:
Primary Current (Ip):
Ip = P / (Vp * η)Secondary Current (Is):
Is = P / (Vs * η)- Where:
- P = Output power of the SMPS (in watts)
- Vp = Primary voltage (in volts)
- Vs = Secondary voltage (in volts)
- η = Efficiency of the SMPS (typically around 0.8 to 0.9)
The current density (J) is the maximum current a wire can safely carry per unit cross-sectional area.
A typical value for SMPS applications is around 4-6 A/mm².
The cross-sectional area (A) of the wire is given by:
A = I / J- Where:
- I = Current (either Ip or Is)
- J = Current density (A/mm²)
The diameter of the wire can be calculated from the cross-sectional area by using the formula for the area of a circle:
A = (π * d²) / 4Rearranging for d:
d = √((4 * A) / π)- Where:
- d = Diameter of the wire (in mm)
- A = Cross-sectional area (in mm²)
For high-frequency SMPS designs, the RMS current and skin effect must be considered.
The skin depth (δ) informs us regarding how deeply current penetrates into the conductor and is given by:
δ = √(ρ / (π * f * μ))- Where:
- ρ = Resistivity of copper (typically 1.68 × 10-8 Ω·m)
- f = Operating frequency of the transformer (in Hz)
- μ = Permeability of copper (4π × 10-7 H/m)
For high-frequency designs it is recommended to use multiple thinner wires (litz wire) to minimize skin effect losses.
Now let us see how we can calculate the wire thickness for a 100 W SMPS transformer with the following parameters:
P = 100 W
Vp = 10.29 V
Vs = 330 V
η = 0.85
J = 5 A/mm²Primary Current:
Ip = P / (Vp * η)Ip = 100 / (10.29 * 0.85) ≈ 11.4 ACross-Sectional Area for Primary Wire:
Ap = Ip / JAp = 11.4 / 5 = 2.28 mm²Primary Wire Diameter:
dp = √((4 * Ap) / π)dp = √((4 * 2.28) / 3.1416) ≈ 1.7 mmSecondary Current:
Is = P / (Vs * η)Is = 100 / (330 * 0.85) ≈ 0.36 ACross-Sectional Area for Secondary Wire:
As = Is / JAs = 0.36 / 5 = 0.072 mm²Secondary Wire Diameter:
ds = √((4 * As) / π)ds = √((4 * 0.072) / 3.1416) ≈ 0.3 mmIf the operating frequency is high (e.g. 20 kHz or higher), consider using litz wire to reduce skin effect losses.
Make sure to use multiple strands of thinner wires with a combined cross-sectional area equal to the calculated area, and avoid using a single thick wire.
Wrapping up
In this post I have explained how to calculate and design ferrite core based inverter transformers, using the following steps:
- Calculate primary turns
- Calculate secondary turns
- Determine and Confirm Bmax
- Determine the maximum secondary voltage for PWM feedback control
- Find primary secondary turn ratio
- Calculate secondary number of turns
- Calculate auxiliary winding turns
Using the above mentioned formulas and calculations an interested user can easily design a customized ferrite core based inverter for SMPS application.
For questions and doubts please feel free to use the comment box below, I'll try to solve at an earliest
More Information can be found under this link:
How to Calculate Switching Power Supplies
Thanks for always
Pls, I planned to make DC to DC 12v – 300v voltage voltage booster using push pull configuration.
So now, my push pull secondary side outputed voltage rating 900ACV, then I use UF5804 in form of bridge rectifier with additional 450v 47uf capacitor
But unfortunately my DC output is around 50DCV, which is very wrong
Pls help, am confused
Atiku, It seems your 900V AC reading is incorrect if the rectified DC is showing as 50V DC. Please recheck the AC voltage with a load connected.
If you are not getting 300V DC output, it means your winding calculations are not correct….
Please calculate them again, and check the response.
🤔🤔
I will try and check it😔
Sir, you’re so amazing
Your explanation is easy to understand, thanks a lot
Pls can I have your whatsapp contact, pls 🥺
Thank you so much Atiku, Glad you found my explanation helpful.
You can absolutely Feel free to discuss whatever circuit related issues you have on this comments platform, I will try to solve it for you as much as possible.
Pls I need a explanation on how to modify this Ac -DC 19v 3A adapter
To a 5.2v 50A
If you are looking for a switching regulator, then you can calculate the parameters as suggested in the following article:
https://www.homemade-circuits.com/calculating-inductor-value-in-smps/
This circuit you can use it at the output of your adaptor to get the 5.2V DC
50 amp is impossible from a 3A source…
Thanks I will go through it
Thank you Sir
sir this is incomplete information
please mantion transformer kw size wire size
or for 50khz frequency
500w tranformer core size
plz
Mahendra, I have updated the article with the required information…
shir hamko pcb banwana hai plese help 7607919707
Kanhaiya, sorry I do not manufacture PCB nowadays, you may have to find other online sources.
Thank you so much Sir. your article was very insightful and easy to understand. However there’s a part i wish to be clearified on. You got ur primary turns to be 3 turn. So during rewinding, is the center-tapped point at 3 turns making the end to end 6 turns ? or the center point in 1.5?
Thank you Noel, glad you found the article helpful.
The 3 turns is for each half winding because in a center tap transformer each half winding would be subjected to the mentioned 10.5V DC separately, so 3V rating is for each half winding, meaning the total winding voltage would be 6V.
Hello Sir,I try to make DC CDI ,id don’t know how to calculate ferrite core transformer windings FYI,*…12DCV input and 220vac output…pls help me to solve the problem… Thanks a lot.
Hello Zulkafli, I have a DC CDI circuit in this blog with the winding details, you can refer to the following post:
https://www.homemade-circuits.com/dc-cdi-circuit-for-motorcycles/
Hi,
How you increase the power by connecting transformers in inverter?
Hi, you can increase the power by increasing voltage and current rating of the transformer.
Voltage can be increased by increasing the number of turns of the winding, and current can be increased by increasing the wire thickness of the winding.
How to build resonant isolation transformers
I have a 3kw SMA solar system. I suspect it of emitting RFI as I have had some anomalies on some small electronic ccts. The only test I have been able to do is bring a portable radio, between stations, near it and I get a large increased static. My research suggests that it might be fixed by placing a snap on ferrite core around the input/output wires. I am not sure which ones would be suitable if any. I hope you may have some suggestions or point me in the right direction.
Thanks
Kindest Regards
John Dean
Actually RFI suppression is best done by having EMI filters inside the circuit itself, however, since it may not be possible for you to open the solar controller and do the modifications, the simpler alternative would be to attach a ferrite core suppressor on the cables.
I think you can use the ready-made ones which are available on amazon, such as this one:
" rel="ugc">
Any similar type can be tried, which fits snugly on your system cables.
As we know number of turns primary and secondary how to calculate wire guage/size for winding in primary and secondary? OR
Which guage number wire we can use for primary and secondary?
The best way to find it is by practical experimentation. For example a 1 mm wire can easily handle upto 4 amp current, similarly a 2mm wire can handle upto 8 amps and so on.
Another way to find this is by referring tot the following article.
https://www.homemade-circuits.com/56492-2/
How can the power rating of a ferrite transformer be determined?
The power rating is mainly dependent on the wire thickness, I do not have a formula for determining the power rating.
Hi. Thanks for this article. I am building an inverter circuit that will have 12 volts supply and an AC output with 10 kHz frequency. The AC output voltage will have to be adjustable from 0 to 10 volts peak. I’m using the SG3525 IC to drive 2 MOSFETs in push-pull topology. So, I will have to make a transformer with ferrite core and wind a center tap primary. I am using the calculations in this article as a guide. Am I correct to assume that I should be able to get my required variable ac voltage at the secondary by controlling the pulse width of the SG3525? I found out that the duty cycle on each of the SG3525 output can only change from 0% to 45%. Thanks, and looking forward to your thoughts.
Hi, Your assumption is correct, the secondary RMS voltage of the transformer can be proportionately altered by modifying the PWM of the IC SG3525. 0 to 45% is enough to generate a significant change across the output RMS, although not upto 0V.
As I said before you will have to work hard and figure them out yourself….
The secondary turns is already given in the discussed article, you should read it carefully:
https://www.homemade-circuits.com/smps-2-x-50v-350w-circuit-for-audio/
I’m finding it difficult where the core area is 40mm x 40mm and I’m getting 0.***** Turns
I just found the answer to my question about your calculation for Bmax using 4 and others using 4.44. From what I have found, if you are using a sine wave to drive the primary you use 4.44. If you are using a square wave to drive the primary then 4 is used instead. I found this by chance while reading the article at the link below when looking for answers to other questions. Just figured I would post back to let other readers know this too. Sorry to bother you, and thank you for this helpful article.
Choosing Core Size
Thank you for clarifying the point, appreciate it very much!
Hi, I was just noticing in the (Primary Turns) section of this thread that after you come up with 3.2 turns, round it to 3 turns, and then recalculate Bmax to see if it is in range, the formula you use has (4 x F x Npri x Ae) in it. However, in most of the Bmax calculations I have seen elsewhere use (4.44 x F x Npri x Ae). Your calculation comes up with Bmax=1600, but using the other comes up with Bmax=1441.441 which is a bit of difference. So, my question is am I missing something or is this just a simple mistake?
Hi, the number 4 is used for square wave application and 4.44 is used for sine wave applications. Since a square wave is assumed in the above calculations, we have used the number 4.
Hi again Swagatam. You referred me to the article below which is very informative, so many thanks for that, but I am still a little confused on how to proceed in my choice of core size and wire size for a 1KW ferrite tranformer.
Many of the comments below seem to be asking the same question. How do we determine the size of the primary and secondary wire csa from the power we require?
For example the figure of 3 turns on the primary in your example doesn’t appear to relate to any input current calculations, although varying the number of turns and size of wire csa on the primary would alter the input current and hence ultimate power of the transformer and either be posible or imposible to construct ( due to thickness of the wire) on any given core size.
As you also state that it is important to correctly balance the core size with the delivered power to ensure neither saturation or under utilisation of the ferrite core there would obviously be a great deal of practical use for a design calculator where we could enter the parameter of input voltage, output voltage, frequency and power required and then the calculator delivers the optimum core size, numbers of turns for the primary and secondary windings and wire csa of both. Does any core manufacturer actualy provide anything like that to your knowledge to reduce the need for an experimental approach?
I used the tutorial to determine that for 240v RMS (not 220V as in the example) I would need a transformer secondary delivering 340V (peak) + 20v (headroom) = 360v. I have also determined that from a 10.29V (low 12v battery again from your tutorial) source I would require a 35:1 step up ratio, hence if using 3 turns on primary I would need 105 turns on the secondary. The ETD49 ( the largest) core in the datasheets you sent suggests a maximum of 692watts, so is a 1KW transformer something that is difficult to construct?
I see below that others are suggesting multiple parallel tranformers.
Can you also put me on the right path of where to start for determining the csa of the wire I require?
I guess the reactance of the 3 turns is a measure that would be useful and then I could probably calculate the current at a given frequency using the inductive reactance formulae 2piFL. Is that right?
But how do I determine the inducatanec of 3 turns without measuring it with an inductance meter that I don’t possess?
This is where a calculator would be handy and my knowledge is lacking.
Thanks for your help and comments.
Steve
Thank you Steve!
I understand that providing wire thickness calculation is important, however presently I don’t seem to have any information regarding this with me. The only related software which I have with me is the following one, but I am not perfectly sure if this may be relevant and helpful:
https://www.homemade-circuits.com/56492-2/
The other method is to try through a trial and error method.
For example we can assume that a 1 mm copper wire can handle upto 5 amp current, so with this yardstick we can estimate the approximate wire thickness for the primary and the secondary winding respectively.
I don’t think inductance would be crucial if the number of turns are known to us.
I hope this helps!
Another interesting link Swagatam and thanks again, but I am now more confused 🙂
Maybe I am reading the table wrong.
If my inverter is running at the optimal frequency just above the audio range then the line 20 figures for 0.911mm wire would seem to be my best choice, since it gives a figure of 27Khz to avoid skin saturation. Diameters above that increase the current handling at the expense of frequency compatibility for the design.
Line 20 in that chart for the 0.911mm wire also gives the maximum current for power transfer as being 1.5A.
Since in my 1KW tranformer I calculate I need a current of 1000W/12V = 83 amps!
How to wind a coil to handle 83 amps whilst ensuring other parameters remain within the quoted cable limits?
My comment regarding inductance measurement was purely to try and determine the reactance since I would have thought that in order to be able to get sufficient current flowing in the primary I would need to ensure that the inductive reactance is minimal?
I (Current flowing in the coil) = V (voltage applied)/XL (inductive reactance at the given frequency determined by 2piFL)
XL =V/I = 12/83 = 0.144ohms
Doesn’t that formula apply in this instance?
Thanks again
Steve
Thank you Steve,
I don’t think I will be able to provide any useful suggestions because my knowledge regarding wires and inductors is not so good.
That is why I feel trying through trial and error is probably the best way to go.
According to me the frequency is related to the number of turns and current handling capacity is related to the wire thickness and these two parameters are not related with each other.
The reactance can be probably kept minimal by using bifilar type of winding in which many thin wires are wound in parallel instead of using a single thick solid wire. I am not sure about this I may be wrong.
what is shape of output voltage signal?
I know this is not actually on topic for this article but I would like to ask your O.P. on the efficiency differences between Push/Pull and Full Bridge. Also I’m looking for a source for Ferrite cores such as the mentioned piece in this post. I want to construct some Xformers to convert a 12Vdc supply to 120Vac. I think 250w units are a good practical size to work with as they would work nicely with a power board/EGS002 system, use 4×250 Xformers to equal a 1kw and so on, 8×250 for 2kw etc. I’m looking at some 1kw power boards to assemble and also some boards with either 20 or 24 MOSFET’s, so if I use MOSFET’s capable of driving multiple 250 watt sub step up units connected in parallel. I think you can see where I’m going with this. I want a modular system and the way I see it is if the load is spread over the complete system under low level, current draw is simply lower and as the load increases, so does the primary current draw since the Feedback Vreg part of the system keeps the output stabilized by adjusting the PWM?
Thank you for your question! Push pull or center tap transformer is less efficient than a full bridge simply because the full bridge does not need to have an extra winding and therefore can be compact and more efficient.
Hm, that part about the winding having to be configured for the opposite side didn’t even register in my thoughts before. I had an inverter that went up in smoke some years ago due to a lightning strike to 1 of my turbine towers. A 2kw 24vdc/120vac unit, modified wave, and at first I didn’t realize a problem was developing because the unit was still functioning but at a lesser output level. Some of the transformers in it had melted and the PCB had a portion of it burned out in the center of the board. Those transformers were wound with a center tap primary and 2 lead outputs. That inverter was a high freq low DC to high DC level then switched to 58 hz… I though it odd it had a 58 hz output according to the meter I left plugged into a wall socket in my cabin as a way to monitor power from the inverter to the cabin. But now that you have cleared this up, it makes sense now, I can live with the lesser winding part along with the lesser bulk that would be present simply having to use twice as much wire. Now I’m wondering why anyone even bothers to use the push/pull method. So far I can’t see any appreciable component count difference but I have placed a schematic of either side by side and confirmed. Now on to finding a source for ferrite cores suitable for my planned project.
Thank you Bret! Inverter using a center tap transformer is actually super easy to build. You can see a few examples in the following article:
https://www.homemade-circuits.com/7-simple-inverter-circuits/
On the other hand full bridge inverter circuits are a bit more complex to build, comparatively.
I need to understand about the headroom voltage pls
Thanks a lot this was very helpful
The way most inverter manufacturers do this is to simply use mulitple Xformers in parallel to get the final output value. Such as in your case of 1kw, this article covers a 250w Xformer, simply make 4 250w units, use a driver circuit for each Xformer and connect them in parallel. input to the next input and each output to the final point. Doing it this way the case can be maintained at a lower height yet make the inverter wider and longer. This would be a requirement anyway simply to address the added switching components on the board. The other way to do this would be to make more smaller boards and stack them or line them in rows and connect them to the inverter controller board, such as the EGS002.
Please sir how do we calculate for a 1000 watt transformer?
Secondly, how do we know the size of coil to used?
Wire thickness and size will need to be experimented, it is not mentioned in the above article. The above article only discusses the number of turns.
Ok sir what will happen if I use same wire thickness on the primary and secondary side of the transformer but with different turns based on the calculation you gave?
Nothing will happen, it will still work, but your transformer will become unnecessarily bigger in size. Primary winding should have proportionately thinner wire thickness than the secondary.
Thanks for the word proportionately, it says a lot; does it mean the wire section area?
but i don’t get it…thinner wire on the primary of a step up from 12V to 310V?
It should be thicker wire for the 12 V side and thinner wire for the 310 V side.
Thank you for a very helpful Ferrite transformer guide.
I was able to create a worksheet to verify your results as well as insert values for a toroid core from Magnetics Inc. which confirmed the values I have been using to create a higher power inverter at higher frequencies using home made litz wire with 0.25mm diameter awg30 enameled wire.
Calculating power handling capacity has been a bit of a grey area for me and though Magnetics has a nice guide for power handling for their cores as 15KHz, 50kHz, 100KHz and 250KHz for push-pull square wave circuits like this one, I am not sure about the amount of power I can get through the system with a 12V battery. Perhaps I must choose higher voltage FETs so I have the possibility of running off 24V, 36V or 48V to get the higher output powers.
I have two 48613 TC toroid ferrites (85.7 x 55.5 x 12.7mm) WaAc(cm4)=46 AL=3000mH/1000turns which I wanted to double up to get a higher power and one 47313 TC toroid ferrites (73.7 x 38.9 x 12.5mm) WaAc(cm4)=25 AL=4000mH/1000turns Which I hoped to use for the LC filter.
We are suffering severe load shedding and I wanted to at least be able to keep the LED lights in the apartment and my PC going for which 500W should be more than enough.
Do you think the LED lights and PC may work perfectly on 220VDC?
Thank you, and glad you found the post helpful!
Since the PC and the LED lamp are both SMPS devices they might work perfectly fine with 220V DC, provided the power capacity of the inverter is sufficient enough to drive both the units satisfactorily.
Please How Can I Build One Ferrite Core Inverter For My Self At Lease 2.5 KVA?
Wire gauge ka pata nahin chala
Yes wire gauge will need to be fixed with some trial and error. There are online charts which will tell you about the wire thickness and their current handling ratings.
Hì Swag.
The explanation on ferrite transformers is quite elaborate. Thank you for the calculations. Now I’m able to work out my inverter from scratch. I treasure your articles so so much.
It’s my pleasure Antony, Glad you found the article helpful.
I got Np:5 , Ns:204 Bmax:1474 (input 12V)
If I multiply by ×2 (Np:10 , Ns:408 , input 12V) is it right or wrong? And will it affect the output?
hi swag. Have a nice day.
I have tried to operate a ferrite ransformer in inverter push push circuit having 50Khz frequency. i also set the switching frequency of sg3525 to 50Khz. when i connected the load, mosfets become too hot instantly. interestingly, i made another ferrite transformer using frequency 15khz. defininately it covers more turns as compared to 50Khz transformer. When i operate it through the same pwm circuit setting frequency 15Khz, it worked fine. mosfets are cool and no problem. howerver the power efficiency is reduced.
kindly guide me what is the actual problem, why the load not operated in 50Khz frequency operation
Thank you Raees,
For Ferrite core transformer the number of turn calculation is critical with respect to the frequency. If there’s even a slightest amount of discrepancy in the calculation can result in an unpredictable behavior of the smps and heating up of the mosfets. It could be possible that the 50kHz frequency is not perfectly matching the ferrite transformer specifications which may be causing the issue. Another factor is that at high frequencies the mosfet internal capacitance does not get the chance to discharge quickly which results in heating up of the mosfets.
To prevent this you must use very low value gate resistor such as a 10 ohm or 5 ohm, also make sure to connect a 1K directly across their gate/source leads. More information about how to keep the mosfets cool can be found in the following article:
How to Protect MOSFETs – Basics Explained
sir how can i make simple ferrite core e.g 6v-0-6v transformer 200watt also how to reduce winding transformer between primary winding and secondary wanding number turns
Abdoul, ferrite core transformers can be built only through calculations as explained in the above article.
Thanks again
Can you explain me , how to calculate the delivery power from ferrite core transformer?
I Price your help
The power output will depend on the thickness of the wire and the voltage rating of the winding.
Thanks for your explanation
I’d like to know how calculate AWG diameter for each winding.
Unfortunately I do not have the formula for calculating the wire thickness, it will need to be judged through some trial and error.
Dear Sir,
Please sir, how do I check if ferrite core transformer is good in a SMPS circuit troubleshooting.
Hi Godfrey,
The easiest way to check is through a visual checking which will ensure the transformer is not burned. If the taping on the transformer is intact and mot melted, and is without any carbon deposits then the transformer is probably not damaged due to burning. Next step would be to check the continuity using a multimeter, and the final step would be to check the inductances of the various winding of the transformer.
Sir what about output and input current , gauge of wire to be used , and size of ferrite available.
Sanjay, the output current will depend on the wire thickness, which will need to be found through some trial and error. The size of the ferrite core and the bobbin should be such that it accommodates the total winding comfortably inside it.
Thanks great Swagatam ,
I have no frequency meter. I set the frequency by selecting appropriate CT and RT.
Is it right?
Hi Raees, I think the frequency should be confirmed using a frequency meter across the output terminals of the IC, and only then you can calculate the ferrite transformer accordingly.
Hi Swagatam. Thanks for the post. Your all posts are really helpful and informative. Today I would like to ask a question which always confusing me while designing inverter projects. Suppose I made a oscillating circuit using sg3525 ic. I set it’s clock frequency 20kHz. What frequency should i chose while rewinding calculation of ferrite transformer for the same circuit.
Thanks Raees, If the frequency is from one of the output pins of the IC, then the frequency specification of the center tap ferrite transformer should be also 20 kHz.
Hello, I did the math and I need 6 turns primary and 150 turns secondary for a center tapped EE42 core transformer. Is there anywhere I can find how much wire can be fit onto this core? IE what diameters can I use? If there is space left over on the transformer core is that ok? IE the windings do not completely fill the gap between core and thimble.
According to me, the winding should accommodate optimally inside the core, meaning, the winding should not spill out of the core, neither should it be too much inside the core. Unfortunately there’s no math for this, and this can found only through some trial and error. If it does not fill completely it won’t be a problem according to me….you can still try implementing it without any issue. Some space left is OK.
Very good topic thank you for sharing your knowledge;
How to find the size of wire for primary and secondary?
Thank you and glad you liked the article. The wire thickness decides the current of the transformer, which can be probably measured using available online charts.
Thank you very mutch for the good explanation!
But i thing 100mm2 = (√100 x √100)mm =10mm x 10mm = 100mm2 = 1cm2
125mm2 = (√125 x √125)mm =11,18mm x 11,18mm = 125mm2 = 1,118cm2
540mm2 = (√540 x √540)mm =23,23mm x 23,23mm = 540mm2 = 2,323cm2
and so on………..
Good day sir
Pls sir before the coil how can we know the power (wattage) of a ferrite core. I mean the total watts that the core can handle (2) how do we choose b Max and what is the formula ( 3) how do we choose frequency when we are designing transformer that will be used without IC
Hello Samson, the wire thickness and the maximum voltage of the transformer decides the wattage. You can select the wire current handling capacity through online charts, or with trial and error.
Bmax details is given in the article. If you want the exact value then you may have to check the datasheet of the ferrite core.
Any frequency between 20 kHz and 100 KHz can be selected for SMPS.
Ok, thanks a lot for your reply.
But I don’t mean the wattage of the transformer. I meant the wattage of the ferrite core it self.
As in how to calculate the iron or ferrite it self.
The wattage of the transformer is determined by the content of the winding, meaning the voltage and current rating of the winding. The core has to selected such that it accommodates the winding correctly within the cores.
I am so much happy for this topic you have explain.
I would like to ask if this will be possible in making (Designing) a SMPS transformer
for a power supply and how to choose the proper wire size for the primary
and secondary.
Glad you found it useful! Yes, it is specifically intended for designing SMPS transformers. Wire dimension will need to be confirmed from appropriate copper wire current charts
1.Good day sir, please I need inverter circuit for this ferrite core transformer that u I can build at home.
2. Sir I don’t really understand how you got 96 for sec turn?
And how also can I get total number of primary turn?
Thank you sir for the response
Godspower,
I do not have an elaborate design of a ferrite core inverter circuit but you can try the last circuit from this article, and see if that helps:
https://www.homemade-circuits.com/half-bridge-mosfet-driver-ic-irs21531d/
Formula for the secondary turn is:
Primary Voltage x Secondary Turns = Secondary Voltage x Primary turns.
If you have 3 values you can get the 4rth unknown value.
Thanks boss for this detailed explanation, please what’s the maximum power this core(ETD39) can ouput?
Onyeka, the power will depend on how you accommodate the winding and the number of turns on the core. If you do it efficiently you would be able to get the maximum power output from it.
Which means I can get upto 1000w using etd39?
It will depend on the winding content.
Thank you Swagatam
Hi how can i calculate diameter of primary and secondary?
The diameter of the wires will need to be selected with some trial and error or through online charts which tell you the wire thickness with respect to its current carrying capacity
hello Mahdi. Diameters of a wire for all windings of all transformers are depends on load-regime. Below 20-30 kilohertz for per-minute-duty-cycle of load 10-50% is enough 4-5amperes per square millimetre, applicable any single-fiber wire. If per-minute-duty-cycle of load around 40-100% – for relability necessary around 3.5-4.5amp per square mm of wire’s cross-section. If necessary long-time short-circuit-duration must be less than two (2) amp per square mm or less – with correct designed of transformer’s cooling.
If frequency is above 20-30 kiloherts (wery-above 60-80 KHz) are necessary all these:
1-to use multi-fiber’s wire against ‘skin-effect’
2-do not exceed 2-2.5ampere per square millimeter
3-get in count “parasitic capacity” between loops of winding
4-to made as short as it possible all high-frequency’s lines-for minimize “parasitic inductance” – against high-voltage damage of elements. It is not easy because of thermal sink’s sizes and some other limitations.
5-get in count leakages of high-frequency’s magnet field from all elements=dissipation, which can made over voltages in another circuits with overheat of all around – by a geometry = design or by a shields.
Also your converter must not be a source of an electromagnet notices – via set of frequency (50 x N hertz) with correct primary filters with correct designed shields e.t.c.-at any frequency!!!!!!!
good luck you.
thanks great job
i have problem
The calculations do not give me the value of 3.2 turns in the primary
Taking the formula of this guide.
12*10^8)/(4*50000*1500*1.25)= 32
Can you check them in the guide?
So I have a question… My husband wants to know if you take a 220V Distribution electrical Input to 12V 19W EI-4830 Ferrite Core Power Transformer Converter, with the 2 red wires on one side and the 2 blue wires on the other, is it possible to simply switch them? Make them function opposite then their original state?
No it is not possible to switch ferrite core transformers with 50 Hz or 60 Hz, unless the transformer has a huge ferrite core with a huge number of winding turns….
hello Keitha. If you meant Chinese transformer EI48x30 – with connection of 220V-AC supply to exit=secondary 6.3V-winding (yellow-yellow) or to 21V-winding (blue-blue) – you must use a ballast for limitation of current – a capacitor or a resistance or elce. But is STRICTLY recommended to avoid the experiment – via over voltage of 220v (red-red) winding will be broken up in seconds to fire with splash of a melted copper e.g.-even if the ballast-limited current inside of transformer’s limits: 6.3V shell be converted to 3800V at ‘220V’ (red-red) 21V shell be converted to 2300V – very dangerous to life!!!!!
But is you need to change voltage you can use auto transformer’s connection – within current limit of 220V-winding!!!!!!! Just connect colored wires in sequence:
phase-red1. Red2-yellow1. Yellow2-load-neutral.
Or phase(hot)-red1. Red2-yellow1. Yellow2-blue1. Blue2-load-neutral.
Or phase-red1. Red2-blue1. Blue2-load-neutral.
Which one color first or 2nd-by experiment only – voltages at load will be more or less than phase’s voltage in accordance of yellow/blue/both winding’s voltage – simple arithmetical adding. Use AC-voltage meter and 20-50kiloohms 1-2watt resistor as load.
Remind risc of electric shock with ALL autotransformators at all time!!!!
what will be the converter circuit & transformer rating for 12V – 500V DC-DC converter?
I am looking to charge a portable phone which requires 6VAC @ 60Hz from a normal wall adapter. Problem is that I have a 12VDC power source only and it is impractical to run a conventional 12-120VAC inverter just for powering this wall adapter and just to keep a portable phone charged. I think I could solve my problem with something more efficient using a 555 into a (perhaps) 1:1 isolation transformer (phone line on portable phones is connected into power source which is another issue that drives the need for isolation transformer). Can you recommend a particular transformer or instructions with how to wind one which will serve a 1:1 isolation purpose to attach to some of your example circuitry that performs efficiently at the lower Hz of 60cps? Thank you. I assume I could just reduce the power supply of 555 to approach the 6VAC on the output rather than experimenting with winding and re-winding different ratios. And since 6VAC is not exact, just trying to make things simple.
Transformer won’t be required according to me, you can accomplish the results using the following concept:
You can replace the IRF540 with a TIP122, and replace the base resistor with a 10k
The pot can be used for changing the charging speed.
Hello sir,
How to select the core size respective to wattage..
Hello Sinu, core size will need to be verified practically, since it will strictly depend on the wire thickness and the number of turns it can accommodate.
How about none ferrite transformers, are the calculations the same?
For iron core trafos, you can refer the following article:
https://www.homemade-circuits.com/how-to-make-transformers/
hello pefeck clovis. Below 1000-1500hertz calculations are same. above 4-5kilohertz transformer of steel-core will be overheated than burn up too soon – is necessary ferrites or amorf=like a glass steel only!!!!
power is depends on frequency in squad-dependence. Mean the – double frequency = four times rise of power. Triple frequency = nine times up the power. Around 25-150 kilohertz is a upper limit of the chemistry&structure of the ferrite = thermal and other losses slowly go up with linear go up frequency – until came to be inappropriate. It is in a datasheets or via an experiment. It is very incorrect but – 40KHz at 8-9 square centimetre Ni-ferrite 2000 Gauss can transform 2-2.5 kilowatts – depends on design and wire and other.
Hi, I’m just starting in this part of electronics, I like your explanation, so l’m gonna make my first transformer following you calculations, so I have one question, in your picture I can see a center tap for the primary side, it’s necessary, this calculations are for the push-pull topology?.
Best Regards.
Hi, yes it is for center tap push pull topology
Sir, good evening, this is a great article i enjoyed reading it several times. I have a small doubt that HOW CAN I SELECT WIRE GUAGE. PLS let me know, bcoz i need to know how to calculate primary and secondary side current with prefect wire guage. Sorry for my english. Pls reply soon
Thankyou
Thank you srinivas, wire thickness decides how much current the wire can carry, or the current handling tolerance of the wire. You can estimate the thickness with some experimentation or trial and error method, or you can refer to the charts and calculations as given in the following page:
https://www.homemade-circuits.com/56492-2/
Hi.
Can you please give any points to consider if I want to operate a standard halogen SMPS at a higher frequency with a view to applying gentle induction heating to embedded metal parts.
Thanks.
Sorry, I have no idea about it!
Does the formula still works on ferrite cores with air gap?
air gap is necessary for all ferrite transformers, otherwise the cores will over-saturate and create a short circuit
so we cant use toroids ?
torroids and E cores are different, so torroids can be used.
So you mean to say Transformers for Full Bridge topology should have air gap. Please guide how to calculate Air gap for this type of transformer. Your design calculations don’t show it. Thanks
For E-cores you will have to insert a paper gap between the surfaces of the cores that touch each other. Just insert a layer of paper or a layer of insulation tape between the core end surfaces that clamp each other face to face. There’s no critical calculation for it.
Hi There Again
I do design high end audio amps, and sinds short also do put a eye on class D where the multilevel is of mine interest, I have simulate some and the 5 level did has -100dB distortion at 150 watts.
These are also nice for sunpanel inverters.
I did see your transformer calculations but are there also some for resonance smps what I do want, these does have low emi and this is good for aufio amps.
I have some transformers but buying the bigger ones is difficult or I have chinese with wrong specs, much counterfeit there,
I need to calaculate a transformer who give 315 volts 100 mA, 2 x 120 volts 200mA, 1 x 12.8 volts 10amp and possible the 2 x 65 volts 20 amp windings, the others are for a audio tube sullpy like 12.8 volts for heater, this 12.8 volts need regulated to 12.8 volts, the others are far from important what concerns the voltages, may easely by + and – 10 % but heater voltage is critical so used for feedback.
For resonance systems, the is more complicated as with normal smps hardswitch designs.
regards
Hi, I appreciate your feedback, however at this moment I do not seem to have the calculation for resonance SMPS transformer, if I happen to find it will update it for you at an earliest
How to calculate dc dc ISOLATED 57v/57v 400khz 1 kva transformer
Hello your article is very educating. I wonder how to choose the proper wire gauge with correspond to its current.
Thank you, wire gauge will depend on the current specs of the load, it’s like selecting the most suitable pipe for transferring a desired amount of water….you have online tables for knowing wire SWG capacity in terms of current.
Does wire gauge will not affect the number of turns?
I think number of turn is depend on the current and wire gauge
It will affect but not much….that is why bifilar winding wire is recommended in which many thin wires are wound in parallel instead of using a single thick wire. This method allows compact winding and does not affect the number of turns.
By the way thicker wire will also mean bigger bobbin, and therefore the cross-sectional area Ac will also change accordingly
Dear sir,
I have a switching transformer with a blown primary winding. I have the schematic that the SMPT came from. Please can you tell me if you can possibly rewind my transformer or give me a telephone number that I can call I live in the UK and would appreciate and help that you can give me.
Kind Regards
Pete Simmons
Dear Pete, I am sorry, I have absolutely no idea about it.
Can ferrite core be used instead of silisium wafer at low frequencies? If used, what are the benefits and harms?
Hi,
Nice article. Thanks for sharing.
I am designing the transformer with following specs; ( just as an example)
Power supply: 12V
Frequency: 50khz
Duty cycle: 50%
Primary : 3-0-3 turns
Secondary: 450 turns
Core: ETD39
Assuming all the above conditions ideal ( meaning no change in the voltage, frequency, etc) will I get 1800V at the output?
Hi, If you got the shown results through proper calculations then definitely it will provide you with the intended results.
Good day sir. How do I calculate for the primary and secondary turns wire guage(size).
Fredstev, the gauge can be determined through gauge chart online…or from this article:
Wire Current Calculator
How do i calculate the area of a PQ ferrite core or a circular core
The area of the circular core should be equal to the Effective Cross-Sectional Area that is referred from the linked datasheet.
Hi
thank you for your good website and perfect information.
i wanna know about details of transformer that used in 12v DC 2Amp power supply (wire cross section, how many turn do i wrap and ..) please help me
thanks a lot
Hi, you can refer to the following article;
https://www.homemade-circuits.com/12v-2-amp-smps-circuit/
Hello and thank you for your good website. Please make the 500 watt inverter with pcb
Please help me to make an inverter at home. Thank Farhad from Iran
Thank you, you can use any standard oscillator based inverter circuit and upgrade the MOSFET, transformer, battery appropriately to get 500 watts
I also know the dc bus voltage.(540v) and output voltages. Just current is missed.
What if i recognize the mosfet and frequency? Give me a clue please.
It can be very difficult to provide a common clue, because SMPS have different topologies and transformer configurations, therefore along with the frequency, the configuration setting will also need to be matched.
In the other hand .if i have a chopper transformer with known outputs , how Is it possible to design a new oscillator ?
Dear Mr swagatam
Sometimes i try to repair vfds or some other circuits wich smps section is completly destroyed. Output includes different voltages with different watts.
I have an idea.. since most of the time the pwm section and mosfet is destroyed and chopper transformator and output section is safe so is it possible to just design a comprehen pwm maker and replace the pwm section and use the same chopper and output section to run the supply?
I have tried this before with uc3842 and 2sk3878…few success . Thanks
Dear Ehsan, If the voltage, current and frequency are correctly matched then probably we can replace them, but without proper calculations it can be a lot risky to try this.
swagatam sir i want atx transformer turns caliculation ratio primary and secondary side. with rughf diagram .
Hello Sir,
I have questions for smps circuit.I want to obtain -12 v in this circuit. How can I design in this circuit.
Thank you so much.
Hello mehmet, you can probably do it by modifying the secondary as done in the following concept:
https://www.homemade-circuits.com/smps-2-x-50v-350w-circuit-for-audio/
Dear sir,
Can we connect the high voltage side of this ATX transformer to ac mains supply (50hz) for battery charging purpose?
(Mains supply is 50hz and our transformer is 50khz that’s why iam ask).
Shabeer, you must have an oscillator circuit with correct frequency with the ATX transformer, otherwise the transformer may burn
If we add an oscillator circuit can we do the inverter function with battery charging purpose.?
May be you can, but I don’t have the full circuit diagram for your requirement.
Sir How to I select winding wire gauge.please help
You can select through copper wire current charts…
why primary wires winding together
example – 0.7 x 4
0.7 x 4 = 3+3 Primary turns
I see it most YouTube videos
Dear Swagatam,
Thanx for explaining it in a simple way.
I am looking to develop a Ferrite Core transformer up 15KW with Max output Voltage upto 125KVp and should operate on 40KHZ freq.
Can You help ?
Thanx and best regards.
Thanks Sudhir, The explained procedure and the Formulas will be the same for your application also, you just have to apply the mentioned formulas stepwise, by putting the relevant figures into it, to get the final results.
Mr. Swagatam,
First of all let me say that you possess extensive knowledge of electronic design.
I have read your article related to smps transformer design.
My question is: With the core size being the only available measureable parameters, such as of a
pull-out Ferrite transformer from a defunct power supply, will this
suffice to successfully calculate number of turns of various windings.
I would appreciate your reply.
Regards
Azhar
Thank You Azhar, Glad you liked my post, although the data was taken from another online website article!
You can try the following general formula
N(prim) = Vin(nom) x 10^8 / 4 x f x Bmax x Ac
In the transformer you can manually winding and find out the N(prim) turns, frequency will also be known, and Ac can be determined by measuring the ferrite core manually. Bmax can be assumed to be 1500…finally you can calculate the Vin value.
Sir again I want to ask how do I know the area and type of a ferrite transformer salvage from scrab board
The rule of thumb is that the winding must fit inside the transformer comfortably, then you can assume that the size is correct.
Goodday sir please I need help, I rewind a ferrite transformer for a 12v inverter using sg3525, that is high frequency inverter I noticed that when I connect my transformer the frequency will be fluctuating and some times there Will be out while sometimes there’s no output and sometimes both mosfet will be hot whli sometime only one will be hot even if I vary the frequency the problem still happen, but if I remove the the transformer the sg3525 will function normal please what could be the problem and possible solutions
Good day Faith, sorry without practically checking, the problem can be very difficult to judge.
Should I send you the waveform that show when the transformer is connected because when I connect the transformer pulse changes drastically because frequency increase, what causes the frequency to increase
The problem may be due to inaccurate winding configuration which cannot be diagnosed with waveform images. Ferrite transformers require perfect calculations in order to work correctly.
For torroidal core transformer how can i calculate nr of turns for primary and secondary?
thank you Swagatam
Sorry, I do not have the details for torroid coil calculations
Copper wire gage is not mentioned
Vd = 0.5V (auxillary winding)
the 0,5V is for one diode rectifier! i have 4 diodes bridge rectifier so i can put 2v to the formula?
thank you
Sorry did not understand your question? 4 diodes will drop 2V, and you may get 0V at the output
OK, yes I just missed that Vd is specifically for compensating diode drop…yes that’s right!
Hello Swag i have a problem with the auxiliary winding for the pwm! does it works only in +33V or i can make it work with only +30v? is there a limit for the voltage?
Hi Mathieu, there’s no limit for the voltage value, you can set it with the help of the given formula.
Hello
How can I specify the output current and also the number of the wire used in a SMPS? For example, I want to design a SMPS with 12 volt and 10 amp output, how I can specify the size of the transformer and also the number (diameter) of the wires for two sides?
Thank you
I am not sure about that, perhaps this table can help
https://www.homemade-circuits.com/56492-2/
It has to be done through some trial and error by making a sample transformer first and checking the current and then modifying it proportionately
Dear master
Although the article wasn’t the same respond that I expected (it mostly speaks about the resistance of the copper or aluminum wires) nonetheless thank you for your answer.
Let me I pose my question otherwise:
Dose the number of turns (for an specified output voltage) depend on the amount of the output current (amp), or current is an independent factor to voltage. in the other word, for obtaining a higher current for a specified voltage, does the number of the wiring turns remains changeless but the size of the transformer become larger?
Mans, once the number of turns are calculated for the specified voltage, the current can be optimized by appropriately dimensioning the thickness of the wire. This must be optimized by winding a bunch fine copper together instead of using a single thick wire, to eliminate skin effect.
Thank you Mr. Swagatam
I knew this technique previously, because I not only made a few traditional transformer (with iron core) years ago, but also repaired a few elector motors with burned winding that one of them was a 220 v, 10 amp motor with 1 mm wire. As I hadn’t the necessary equipment and tools I made all its winding with a piece of flat wood and four nails!
At that time, I had a table that guided me how to choose the different double thin wires instead of a single thicker one.
Also I had a formula that offered me the size of the proper transformer and wires for a specified current, but now I forget all, while winding a ferrite transformer is different with an Iron one.
I wanted to know technically, what the ratio of the size of a ferrite transformer and the thickness of the wire (for achieving a higher current with the same voltage) is?
I think, Ac in the formula is the same transformer size (that can be changed for a higher current) but there is no point in the article, about the appropriate diameter of the wires in regard to the transformer size.
Also you spoke about the skin effect (probably the thickness of the isolating resin of wire), what it is?
Sorry, I don’t have the ratio formula for the ferrite core size to wire thickness…this has to be fixed with some trial and error method so that a benchmark ratio can be determined.
Skin effect happens for thicker single wire winding where the electromagnetic induction does not get absorbed deep into the secondary wire, resulting in inefficient current transfer. To correct this many thin wires are used in parallel for the winding instead of a single thick wire
Yes sir! But how do I calculate the power of the toriod ferrite core. Thank you Sir!
The power of transformer depends on its voltage specifications, and the current handling capacity (V x I). The current handling capacity depends on the wire thickness.
Hello Swag i have found the teslas value for my etd34 Bmax = (330 mt),(0.33T),(3300Gauss). with your formula,bmax is in tesla,does we calculate in mtesla , or in gauss(3300)?
Thank you
Sorry Mathieu, I have not yet investigated Tesla value, so can’t suggest much on this.
Hy Swag can i fix the peak value (sec turns) at 115V?
Hi Mathieu, yes you can….
Hello Swag for the windings of the ferrite transformer do you made it manually or do you send your transformer to a specific factory ?
Thank you!
Hello Mathieu,
if you have experience with coil winding and have a winding machine then you can do it yourself, otherwise you may have to contact a transformer winder.
hello Swagatam,
can you please help in full bridge transformer design 1200 W ??
whats your email id and how to connect you ???
Prachi
Hello Prachi,
I would prefer discussing the topic here through comments so that others can also benefit from it. Hope you don’t mind.
I have a full bridge related article which you can refer in the following link. A much simpler design is possible if P channel mosfets are used for the high side mosfets.
https://www.homemade-circuits.com/simplest-full-bridge-inverter-circuit/
Let me know if you have more questions
Hello swag i have a question on the choice of Bmax between 1300G to 2000g! Is there a precision on the gauss? Do i need to calculate my windings with only 1500G for any core size transformers?
thank you
hello Mathieu, the value is not critical and can be between 1300 and 2000. It is dependent on the other factors also, and therefore a critical value can never be found. If you try to select Bmax with highest efficiency then that might require the other parameters to be adjusted accordingly, affecting the overall calculations. That is why we have to be satisfied with whatever Bmax comes withing the mentioned range.
Sir, you have a blessing unto us, and you shall increase and multiply sir.
Sir, i need circuit diagram for power bank, that will convert 3.7v to 5v by 1amp. By using 34063 ic and 555timer. Pls sir i need a quick reply sir.
Thanks Ambrose. the circuit diagram of a boost converter using IC34063 is already given in the datasheet of the IC with formulas….so you can check the datasheet and easily make it from the available information.
Does that mean using the 10k pot, or is there something else i have to do for the 393 that i will not do with 741? What i mean is, how do u mean configure the output of the ic? Thanks for all ur previous replies, i’m greatful.
Just connect a 10K from IC output pin to positive line, that’s all rest everything can be same!
Thanks. Can i use IC LM393 In place of IC 741?
Yes you can use it, just make sure to configure the output of the IC correctly
Do u have a link where i can get a visual description(schematic)? I was getting to understand but i got lost when u said, “Used as the feedback with the inverter ic”. i will be using ic cd4047 how do i connect the aux feedback to the ic? (if diagram is not possible, (sorry to say) but theory will work fine also).
You can check out the diagram just above “How to Setup” in this article:
https://www.homemade-circuits.com/arduino-pure-sine-wave-inverter-circuit/
The bridge input can be connected to the auxiliary winding. Only one transistor is required for your application at the output whose collector could be linked with the R/C junction of the 4047 IC for overvoltage/undervoltage cut off actions
Sorry for the mutiple questions swagtam, but in the feedback aspect of the article, i was thinking if it means to add the other feedback system found in the feedback link, using 555 timer ic? Simply put should i add the 555 ic feedback system to my ferrite transformer inverter?
Evergreen, the feedback can be used for shutting down the inverter during a low voltage situation or controlling over voltage etc. For this the auxiliary voltage could be used as the feedback with the inverter IC. In IC 555 for example this can be integrated to pin#5 for shut down.
My main question is, will it be a center tap or a single? If it is a center tap will it be 9V-0-9V (18V) or 4.5V-0-4.5V (9V) For a 12v battery? And is the aux a must for a ferrite transformer?
I have already answered. it can be anything between 9 and 11V, center tap or not depends what kind of inverter topology you are using. For the aux winding details please read the auxiliary section of the article.
9 means 9-0-9, 11 means 11-0-11 for center tap.
for full-bridge this will be 0-9V and 0-11V
Thanks a lot swagtam, i got it now.
Hi swagtam. If u are to use the transformer for a 12v battery should it not be 9v-0-9v center tap? The diagram shows a centertap transformer but u calculated for single 10.5v.
Hi Evergreen, the calculation is not critical, because the output voltage range is not critical and can be anything between 210 V to 240 V.
10.5 V is used because the lowest battery level is taken as 10.5 V here. The transformer primary can be anywhere from 9V to 11V
Hello, am interested in ferrite inverter transformer, pls is there any way I can be getting them?
Hello, I think you can get a complete ferrite core based converter kit from ebay.
Hi thank you for this post i need to know why you said in your post the transformer you had chose has a 250 W but when i read in the datasheet i find that the ETD39 transformer had 450 W
Hi, the recommended size may have a range between 250 and 450 watts, it cannot be a fixed value. Depends how well the winding is optimized
Not to pick it apart but 125mm ^2 is 12.5cm^2. This same thing is pretty much wrote over here with the same mistake for an ETD39.
Can you please elaborate a little more on this?
No need, I am wrong. I was reading these articles with idea there are 10mm in a cm, But then I looked it up and there are 100mm^2 per centimeter. Didn’t know that. I would delete this if I could. Sorry to trouble you.
No problem, thanks for clarifying!
Thanks for this article. Sir, i want to know where 10^8 is gotten from in the formula for calculating d transformer primary winding number of turn. Thanks.
It’s a part of the formula, a constant.
dear sir! i ‘m using power Esim software for designing smps xformer. i have problem mostly by identifying diameter of secondary turns wire (turns for output voltage let say 16v). they show that N2 = 4 (0.18mm x 7T/W x 9). sir i understand that there are 4 output turns each turn having 9 parallel wire but don’t understand the concept behind (0.18mm x 7T/W)? i don’t know what they mean???
Dear Sheraz, diameter and number of strands is directly proportional to the current specification of the transformers or the secondary of the transformer. Higher current will require proportionately thicker gauge wire and number of strands
it means that there are 7 strands of wire having diameter 0.18mm and each (0.18mm x 7T/W) must be considered as single wire for higher current and then 9 such wire must be winded in parallel for 4 turns?
That’s right, 7 strands together must be considered as single wire for the winding.
dear sir! can this formula ” Ns(pri) = ((Vin * 10^8)/(4 * Bm * fosc * Ae)) can be used for winding smps transformer for single power mosfet smps based on uc3842 etc?
Dear Sheraz, it can be used according to me!
1. That’s with the capacitor connected in series with the transformer, does it help to provide inductive reactance?
2. And if so that it helps to provide inductive reactance, removing the cap then, where will the inductive reactance come from since current will only flow in only one direction when the cap is removed because the cap is charged and discharged through the transformer?
Capacitor works like a series resonant circuit for optimal performance of the inverter
Is it safe to remove the capacitor?
And if you did, will the circuit still work?
If the primary is wound with correct calculation then you can remove the capacitor, otherwise it can burn the MOSFET
hello Mr. Swagatam!
Thanks for the ferrite core transformer calculation. I have seen this same calculation for ETD39 ferrite core transformer in more than 3 blogs. And when i take the idea of the Bmax of 1300G to 2000G for bigger size ferrite like EE65 ferrite with Ae = 540 millimeter square = 5.4 centimeter square, I ended up getting funny number of turn(s) like 1.7Turn = 2Turns approx for a primary voltage of 24V, a frequency = 50KHz, Bmax = 1300G, and Ae=5.4 centimeter square. And since 1300G is the lowest range of the spec (i.e 1300G – to – 2000G), if i say let me adjust the Bmax to something like 1500G so as to be within the middle region of the Bmax spec, the I got 1Turn approx for primary winding.
You know the funniest thing here? the leftover spaces in the transformer can still accommodate like 5Turns for the primary even after considering the secondary. And being a large size ferrite core transformer, I need to have it well wound by ensuring there is no gap between the cores and the winding to avoid excessive losses.
For this reason therefore, I tried to recalculate for Bmax using N-primary = 5Turns and I got Bmax to be 444.444 = 444G approx. So, my question is can Bmax be reduced to such small value for a large ferrite core transformer?
Thank you my mentor for your expected response.
Hello Kingsley, If all the parameters are correctly selected then the turn number will be correct, but if one of the parameters is wrongly selected then the turn numbers can go wrong. Are you sure EE65 is correct, and also the thickness of the wire that you may have selected?
Bmax = 444 will not work as per the rules, so you cannot change that, instead try changing the other parameters which could be perhaps wrongly selected.
Good to here from you my dear motivator.
For the parameters, EE65 is a large ferrite transformer. with all the research i have made, the Ae=540mm square which by conversion is equal to 5.4cm square. For other parameters such as frequency, I chose F=50000Hz, V-in(norm) = 24V, and Bmax = 1500G, yet I got 1Turn for N-primary.
so my calculation was as follows:
N-pri = (24*10^8)/(4*50000*1500*5.4)
Again, I observed that the larger the size of ferrite core transformer, the larger the Ae in mm square. And this is one problem why the Number of turn is drastically reduced. If any parameter spec for the EE65 is wrongly selected, then it should be the Bmax since the datasheet declares Ae to 540mm square.
Hope I am correct saying that 540mm square = 5.4cm square? Or am I wrong? please correct me if i am wrong.
if i should refer your question in the above reply i.e “Are you sure EE65 is correct, and also the thickness of the wire that you may have selected?” I used 10 strands of 20AWG copper coil for the Primary side (i.e 24v battery side) and 5 strands of the same copper coil on the secondary side (330Vac side). Yet 1Turn is too small and enough space still exist in the window area.
Hello Kingsley,
The formula results are dependent on the turn ratio between the primary and the secondary, and also the E core selection. If your wire thickness and turn calculation are not correct then the core size will also be not correct, and this will ultimately result in the whole calculation going wrong.
How much space is left is not relevant to the number of turns on the primary.
By the way using 20 AWG for the 220V is grossly wrong, how can you have a 330V winding wire having the same thickness as the 24 V primary, that too 5 strands together…? I think this is main problem behind the wrong primary turn results.
Please divide the primary wattage with secondary voltage to get the secondary current and then you can estimate the wire thickness accordingly.
Ok, I want to ask if the ferrite core transformer will be OK at the frequency of 27KHz since the range of frequency specified is between 20KHz to 500KHz? If that can be fine, then reducing the frequency will take care of the wrong number of turns while still maintaining the Bmax within that same range of 1300G to 2000G; since I can now Obtain up to 2Turns for the primary Turn.
yes 27kHz will work, but using similar SWG wires for primary and secondary would still be wrong, considering the fact that primary is 24V and secondary 330V, the wire must also proportionately vary in thickness.
OK since using the same size of AWG but different number of strands won’t work, can you please suggest me the right AWG for the primary and secondary? Again can you also suggest me the quantity of strands for each?
Thank you sir.
Strands won’t be required for the secondary, since the wire itself will be quite thin. the secondary wire must be 15 times thinner than the primary, considering 24V is 15 times smaller than 310V
Ok, My boss! I will consider doing it as you have said. Thank you dear.
Dear Mr. Swagatam
Thank you for sharing this helpful discussion.But may you discuss about selecting wire tickness (AWG) and wiring transformer(for example first wiring primary then secondary …) due to output current of SMPS?
Thank you
Dear Reza, wire gauge can be estimated with some trial and error (approximation), or you can refer to the table which is given i this article:
https://www.homemade-circuits.com/56492-2/
Normally the higher voltage winding is wound first and then the lower voltage on top of it, with a layer of insulation.
Pls Mr Swagatam, can you help me explain why a capacitor is connected in series with the transformer in the circuit shown from the link below?
http://tinypic.com/view.php?pic=ne9sow&s=9
I understand half bridge transformer connection partially, having read your article about it. But, in the conventional connection used for half bridge transformer connection, there are two capacitors, but in this circuit, only one was used. Why? Does the capacitor act as a power bank, storing power temporarily, to be used for the other half circle when the transistor beneath is switching?
And also, does the capacitor reduce the voltage coming to the transformer?
The circuit shown in the link is not a push pull topology, therefore only a single capacitor is used. Capacitor will reduce the current, not the voltage, higher value capacitors will produce higher current.
Pls can I understand better the what happens in half-bridge, full-bridge and pull-pull connection of ferrite transformers clearly with a bit of diagrams, if possible?
And also, can a ferrite transformer when operated on pulsed DC, still possess reactance to resist voltage and current as would a normal transformer in order to avoid a short circuit when connected to the power supply? Thanks
Half bridge will pass current in only one direction across the primary winding. A full bridge will pass current alternately across the winding in reverse forward way. The output of a half bridge will be a half wave AC, whereas in full bridge it will a full wave AC.
Half bridge and full bridge both can work with two wire primary.
A center tap push pull topology is also a full bridge topology but it requires two winding at the primary with a center tap.
A pulse Dc operation is another form of half bridge operation,and it is possible but the output will be half wave AC.
Please did you mean that you divide into half the value gotten for the primary winding calculation because it’s a push-pull topology?
For example, a primary winding calculated as 20turns will then be divided by 2 to give 10turns because it’s push topology?
You must double it for a center tap topology. if the result is 20 turns then for a center tap transformer primary it will be 40 turns with center tap at 20th turn
Ferrite cores are used NOT because of their high permeability. Actually, ironcores, and especially permalloy cores, etc could showcase permeability exceeding that of typical transformer ferrite cores.
For the reference, effective permeability of typical transformer core ferrites used in SMPS would usually be about 1000 to 2500 or so, depending on application. Gapped cores, like those in flybacks would have effective permeability much lower than that (though it “coupled inductor” rather than “transformer”). However, transformer-grade steel alloys and especially permalloy-like “low-frequency” cores can showcase permeability well around 20 000, more than 10x higher compared to typical transformer ferrites. Some “special” ferrites also expose permeability about 15 000 or more, but are NOT used for transformers, being high-loss things, so only suitable for ferrites. Who needs high-loss transformer? It would just heat itself up, wasting power on that. Avoiding this scenario is pretty much goal of transformer calculations, especially when it comes to ferrite type selection, etc.
But what makes ferrite transformers small? And why we need ferrite? Its mostly about high frequency operation and eddy currents.
Generally, the higher operating frequency is, the more power could be pushed through same transformer size. So if we want small but powerful supply, we have to go for high frequency. At high frequency one can make far less turns in windings, yet they still would have enough inductance to “resist” incoming voltage. The higher frequency, the less turns we need, the smaller transformer we can afford. To certain extent.
What’s the problem with steel, permalloy, etc? Being metallic they are inherently conductive. At which point, core could act a bit like some kind of (shori-circuited) winding, heating itself by eddie currents. This effect could be put in use, giving a rise to “induction heating” – but we do not want it in transformers. So transformer steels are optimized to have relatively high resistance and also split into separate thin plates to reduce eddie currents. However, the higher frequency is, the more pronounced this “induction heating” gets – and even special steel alloys and very thin plates aren’t enough to prevent core heating. That’s where ferrites come into play. They are ceramic materials, so unlike metals they show rather poor electric conductivity. At which point eddie current loses are mostly mitigated, so we can increase operational frequency a lot compared to steel designs. This implies far smaller windings, so we can push way more power without increasing transformer size. So SMPS would have unusually small ferrite transformer for given power, compared to low-frequency steel transformer designs.
As for topologies, there’re a bit more options. Out of bridge-like, there’re three: half-bridge, full-bridge and push-pull. Half-bridge and push-pull are similar in overall idea, but implementation is different, half-bridge uses just 1 winding and some capacitors to expose winding to both polarities. Push-pull rather uses different halves of winding to achieve same result (in terms of magnetic field behavior). This brings different tradeoffs, and full bridge lacks most shortcomings of both – but being more expensive due to 4 high-voltage transistors reqirement.
Some relatively recent power supply designs could also use e.g. “2-switch forward” approach, which also uses 2 MOSFETs but operates in somewhat different manner. It underuses transformer core, magnetizing it in just 1 polarity, but on other hand it gets favorable MOSFETs voltage and current tradeoffs, pretty much like full bridge, being cheaper solution. So it fairly usual to see 2-switch forward in e.g. ATX power supplies up to about 800-1000W or so. Transformer computed much like “usually”, but with some special considerations in regard of saturation & demagnetizing attached.
There’re also flybacks, that aren’t even transformers by their actions, though turns ratio still haves some meaning. These have their own limitations but are cheapest option up to around ~100W of output power. Above this point different topology could be better consideration though.
Thank you for the nice explanation!
> being high-loss things, so only suitable for ferrites.
Oh, I meant high-loss high-permeability ferrites are used in EMI filters, etc, where turning noise into heat is rather something good.
Also it worth to mention there is approximately the following trend: the higher intended opreational frequency of ferrite compound is, the less permeability it would get, the higher resistivity it would enjoy, it would have lower core losses but require more turns.
As example, think of N49 vs N67, for example. N49 is tailored up to about ~1MHz or even more, while N67 is barely ok up to maybe 200kHz at very most. N67 would have higher permeability, but would get far higher core losses at high frequencies. Overall it comes to trading copper loses vs core loses, in perfect world we would try to hit minimum of their sum, however numerous secondary considerations make it challenging.
Thank you Mr. Swagatam for your reply. Can I understand some better?
Please, what do you mean by Half bridge and full bridge both can work with two wire primary?
Can you explain what this means with the aid of a diagram also?
Thanks
Hello Victory, please read the last sections of this article:
https://www.homemade-circuits.com/how-to-design-inverter-basic-circuit/
It explains about half bridge and full bridge topology in brief.
Hello, I’m Aren from Nigeria, please can You help me on how to know the right frequency for operating any ferrite Core transformer that i wind, thanks, waiting for ur reply.
Hello, the frequency parameter is given in the formula as f.
How do we determine the swg of the coil used
SWG is related to current and can be found by estimating how much current a copper wire with particular thickness can carry. Probably this article can help:
https://www.homemade-circuits.com/56492-2/
Explained in simple and lucid manner, thank you, sir.
My pleasure Ajay, Glad you liked it!