I have explained comprehensively how to build a boost converter circuit for converting a low level DC voltage inputs to a higher level DC voltage outputs. I have furnished all the required calculations s that you can design a customized boost converter circuit.
A Practical Boost Converter Circuit Design using IC 555
This simple circuit is built using an IC 555 circuit for boosting USB 5V to 24V, or any other desired level. The same design can be used for boosting a 3.7 V to 24 V from a Li-Ion cell.

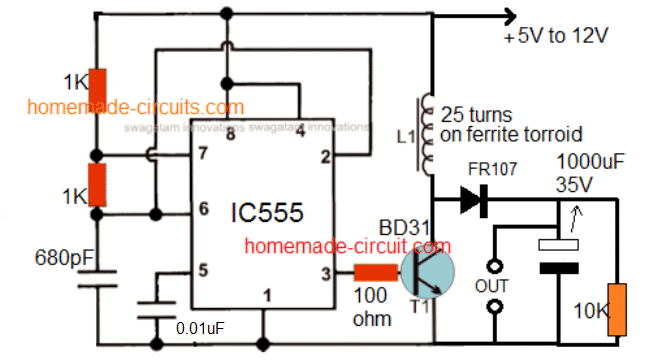
Let's assume we have the following parameters required for the above circuit:
Important Parameters:
- Input Voltage (Vin): 5V
- Output Voltage (Vout): 24V
- Output Current (Iout): 1A
- Switching Frequency (f): 50 kHz
Calculating the Part Values
Step 1: Output Power
Pout = Vout * Iout = 24V * 1A = 24WEfficiency (η) = 85%
Pin = Pout / η = 24 / 0.85 ≈ 28.2WInput Current (Iin) = Pin / Vin = 28.2 / 5 ≈ 5.64AStep 2: Inductor Selection
Inductance (L) = (Vin * D) / (f * ΔI)D = 1 - (Vin / Vout) = 1 - (5 / 24) ≈ 0.79Ripple Current (ΔI) = 0.4 * Iin = 0.4 * 5.64 ≈ 2.26AL = (5 * 0.79) / (50000 * 2.26) ≈ 35µHChoose an inductor with L = 35µH, capable of handling at least 6A peak current.
Step 3: Diode Selection
Reverse Voltage: ≥ Vout = 24VForward Current: ≥ Iout = 1AChoose a Schottky diode, such as MBR360 (60V, 3A).
Step 4: Capacitor Selection
Output Capacitor (C) = (Iout * D) / (f * ΔV)Assume Ripple Voltage (ΔV) = 1V:
C = (1 * 0.79) / (50000 * 1) ≈ 16µFChoose a low-ESR electrolytic capacitor, such as 100µF, 35V.
Step 5: Resistor Selection for 555 Timer
Frequency (f) = 1.44 / ((R1 + 2R2) * C1)Assume C1 = 0.01µF:
R1 + 2R2 = 1.44 / (50 * 103 * 0.01 * 10-6) = 2.88kΩSet R1 = 1kΩ, then 2R2 = 1.88kΩ, so R2 = 940Ω.
Use standard values: R1 = 1kΩ, R2 = 1kΩ.
Finalized Part values for the above 555 boost Converter Circuit
L1: 35µH, 6A
D1: MBR360 (60V, 3A Schottky)
Cout: 100µF, 35V (low ESR)
R1 & R2: 1kΩ each
C1 (timing): 0.01µF
T1 (switch): BD31 or better NPN transistor capable of 6A or a MOSFET (e.g., IRF540N)
Construction Steps (How to Assemble)
Step 1: Build the Oscillator Circuit
Assemble the 555 timer circuit on a breadboard or PCB.
Use the formula for the 555 timer frequency:
f = 1.44 / ((R1 + 2R2) * C1)Select the appropriate values for R1, R2, and C1 to achieve the desired switching frequency (e.g50 kHz).
Connect the output of the 555 timer (pin 3) to the base or the gate of the switching transistor/MOSFET through the resistor (e.g 100Ω).
Step 2: Connect the Inductor and Switching Transistor
Solder the inductor (e.g.35µH) in series with the input voltage and the collector (or drain) of the switching transistor.
Connect the emitter (or source) of the transistor to ground.
Step 3: Add the Diode
Solder the Schottky diode (e.g MBR360) between the inductor and the output capacitor.
Connect the cathode of the diode to the positive terminal of the output capacitor.
Step 4: Connect the Output Capacitor
Add an electrolytic capacitor (e.g., 100µF 35V) across the output terminals for to smooth out the boosted DC voltage.
Step 5: Feedback/Control (Optional)
For adjustable output voltage you can include a feedback circuit with a variable resistor (potentiometer) to adjust the duty cycle of the PWM signal.
Step 6: Add Input and Output Terminals
Solder the connectors or terminals for the input voltage (Vin) and output voltage (Vout).
Step 7: Verify Connections
Double-check all the connections to ensure that there are no shorts or loose connections.
Testing the Circuit
Connect the 5V DC power supply to the input terminals.
Measure the output voltage using the multimeter to ensure that it reaches the desired value (e.g.,, 24V).
Adjust the duty cycle (if applicable,) to fine-tune the output voltage.
Connect the load (e.g, a resistor or a small motor) to the output and measure the current.
Assembly Tips
Use the heat sink for the transistor or MOSFET to dissipate the heat during the operation.
Keep the connections between the inductor, switch, diode, and the capacitor as short as possible to minimize the losses.
Use the printed circuit board (PCB) for getting a robust and reliable assembly.
Adding a Feedback
The above circuit can be regulated with a feedback as shown below:
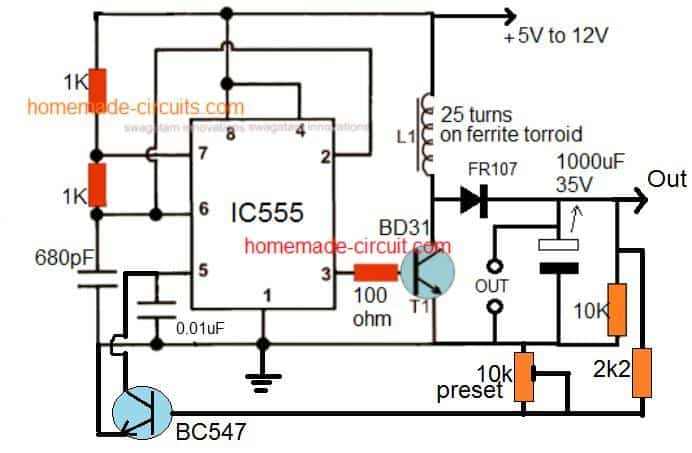
The idea looks quite straightforward. IC 555 is configured as an astable multivibrator whose frequency is decided by the values of resistors and capacitor at pin#7 and pin#6/2.
This frequency is applied to the base of a driver transistor TIP31 (incorrectly shown as BD31).
The transistor oscillates at the same frequency and forces supply current to oscillate within the connected inductor with the same frequency.
The selected frequency saturates the coil and boosts the voltage across it to a greater amplitude which is measured to be around 24V.
This value can be tweaked to even higher levels by modifying the turns of the inductor and the frequency of the IC .
Video Demonstration for IC 555 Boost Converter circuit
How a Boost Converter Works (Theoretical Analysis)
A boost converter is a kind of SMPS or switch mode power supply which fundamentally works with two active semiconductors (transistor and diode) and with a minimum of one passive component in the form of a capacitor or an inductor or both for greater efficiency.
The inductor here basically is used for stepping up the voltage and the capacitor is introduced for filtering the switching fluctuations and for reducing current ripples at the output of the converter.
The input power supply which may be required to be boosted or stepped up could be acquired from any suitable DC source such as batteries, solar panels, motor based generators etc.
Operating Principle
The inductor in a boost converter plays the important of stepping up the input voltage.
The crucial aspect which becomes responsible for activating the boost voltage from an inductor is due to its inherent property of resisting or opposing a suddenly induced current across it, and due to its response to this with a creation of magnetic field and subsequently destroying of the magnetic field. The destroying leads to the releasing of the stored energy.
This above process results in the storing of the current in the inductor and kicking back this stored current across the output in the form of back EMF.
A relay transistor driver circuit can be considered a great example of a boost converter circuit. The flyback diode connected across the relay is introduced to short circuit the reverse back EMFs from the relay coil and to protect the transistor whenever it switches OFF.
If this diode is removed and a diode capacitor rectifier is connected across the transistor's collector/emitter, the boosted voltage from the relay coil can be collected across this capacitor.
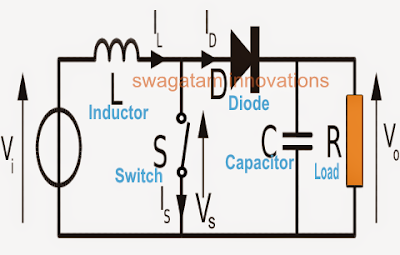
The process in a boost converter design results in an output voltage that’s always higher than the input voltage.
Boost Converter Configuration
Referring to the following figure, we can see a standard boost converter configuration, the working pattern may be understood as given under:
When the shown device (which could be any standard power BJT or a mosfet) is switched ON, current from the input supply enters the inductor and flows clockwise through the transistor to complete the cycle at the negative end of the input supply.
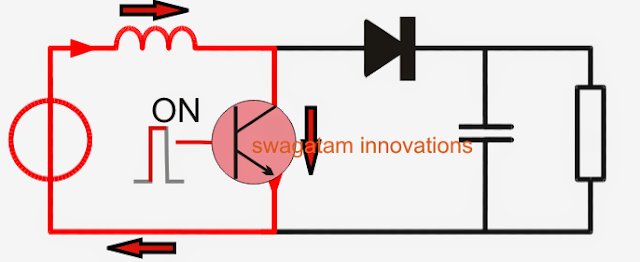
During the above process the inductor experiences a sudden introduction of current across itself and tries to resist the influx, which results in the storing of some amount of the current in it through the generation of a magnetic field.
At the next subsequent sequence, when the transistor is switched OFF, the conduction of current breaks, yet again forcing a sudden change in the current level across the inductor.
The inductor responds to this by kicking back or releasing the stored current. Since the transistor is in the OFF position, this energy finds its path through the diode D and across the shown output terminals in the form of a back EMF voltage.
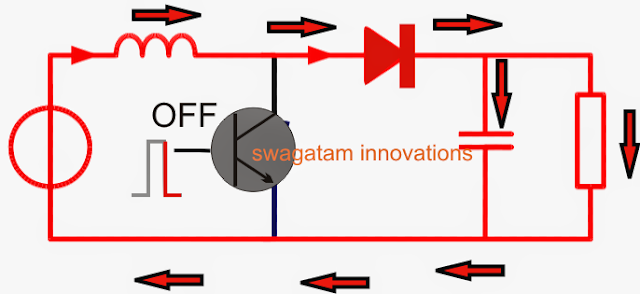
The inductor performs this by destroying the magnetic field which was earlier created in it while the transistor was in the switch ON mode.
However, the above process of releasing energy is implemented with an opposite polarity, such that the input supply voltage now becomes in series with the inductor back emf voltage. And as we all know that when supply sources join in series their net voltage adds up to produce a bigger combined outcome.
The same happens in a boost converter during the inductor discharge mode, producing an output which may be the combined result of the inductor back EMF voltage and the existing supply voltage, as shown the diagram above
This combined voltage results in a boosted output or a stepped up output which finds its path through the diode D and the across capacitor C to ultimately reach the connected load.
The capacitor C plays quite an important role here, during the inductor discharge mode the capacitor C stores the released combined energy in it, and during the next phase when the transistor switches OFF again and the inductor is in the storing mode, the capacitor C tries to maintain the equilibrium by supplying its own stored energy to the load. See the figure below.
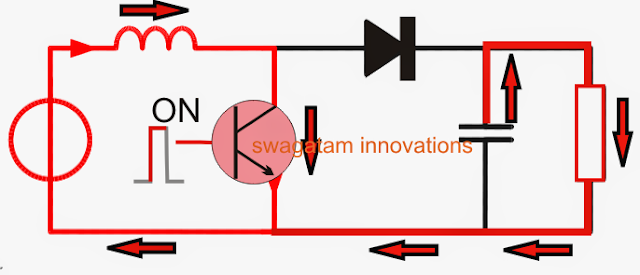
This ensures a relatively steady voltage for the connected load which is able to acquire power during both the ON, and OFF periods of the transistor.
If C is not included then this feature is cancelled resulting in a lower power for the load and lower efficiency rate.
The above explained process continues as the transistor is switched ON/OFF at a given frequency, sustaining the boost conversion effect.
Modes of Operation
A boost converter may be primarily operated in two modes: the continuous mode, and the discontinuous mode.
In continuous mode, the inductor current is never allowed to reach zero during its discharging process (while the transistor is switched OFF).
This happens when the ON/OFF time of the transistor is dimensioned in such a way that the inductor is always connected back quickly with the input supply through the switched ON transistor, before it’s able to get completely discharged across the load and the capacitor C.
This allows the inductor to consistently produce the boost voltage at an efficient rate.
In the discontinuous mode, the transistor switch ON timing may be so wide apart that the inductor may be allowed to get discharged fully and stay inactive in between the switch ON periods of the transistor, creating huge ripple voltages across the load and the capacitor C.
This could make the output less efficient and with more fluctuations.
The best approach is to calculate the ON/OFF time of the transistor which yields maximum stable voltage across the output, meaning we need to make sure that the inductor is optimally switched such that it’s neither switched ON too quickly which might not allow it to discharge optimally, and nor switch it ON very late which might drain it an inefficient point.
Calculating, Inductance, Current, Voltage and Duty Cycle in a Boost Converter
Here we’ll discuss only the continuous mode, which is the preferable way to operate a boost converter. Let’s evaluate the calculations involved with a boost converter in continuous mode:
Inductor Current Build-Up (Transistor ON Phase)
While the transistor is in the switched ON phase, the input source voltage (Vi) is applied across the inductor, inducing a current (IL) build-up through the inductor for a time period (t). This can be expressed as:
dIL/dt = Vi/LBy the time the ON state of the transistor ends and it switches OFF, the current built up in the inductor can be calculated using:
ΔIL(on) = Vi × D × T / LWhere:
- D is the duty cycle.
- L is the inductance value of the inductor (Henry).
- T is the switching period.
Inductor Discharge (Transistor OFF Phase)
When the transistor is OFF, assuming the diode offers minimal voltage drop and the capacitor (C) is large enough to maintain a constant output voltage, the output current (IL) can be deduced as:
Vi - Vo = L × dIL/dtThe current variation (ΔIL) across the inductor during the discharge phase can be expressed as:
ΔIL(off) = (Vi - Vo) × (1 - D) × T / LSteady-State Operation
Under steady conditions, the energy stored in the inductor during the ON phase equals the energy released during the OFF phase. This implies:
ΔIL(on) + ΔIL(off) = 0Substituting the expressions for ΔIL(on) and ΔIL(off):
Vi × D × T / L - (Vi - Vo) × (1 - D) × T / L = 0Simplifying:
Vo / Vi = 1 / (1 - D)Or equivalently:
Vo = Vi / (1 - D)This shows that the output voltage in a boost converter is always higher than the input voltage across the full range of duty cycles (0 < D < 1).
The duty cycle can be calculated as:
D = 1 - Vi / VoPower Stage Calculation
To calculate the boost converter’s power stage, the following guidelines are necessary:
- Input Voltage Range: Vin(min) and Vin(max)
- Minimum Output Voltage: Vout
- Maximum Output Current: Iout(max)
- IC specifications: Choose based on the IC’s datasheet.
Determining Maximum Switching Current
The first step is to calculate the duty cycle at the minimum input voltage:
D = 1 - (Vin(min) × η) / VoutWhere:
- Vin(min) = minimum input voltage
- Vout = output voltage
- η = efficiency (e.g., 80%)
Calculating Ripple Current
The ripple current can be calculated as:
ΔIL = Vin(min) × D / (f × L)Where:
- f = minimum switching frequency
- L = inductor value
Maximum Output Current Check
Verify the IC’s maximum output current:
Iout(max) = [Ilim(min) - ΔIL / 2] × (1 - D)Where:
- Ilim(min) = minimum current limit from the IC datasheet
- ΔIL = ripple current
If the calculated Iout(max) is insufficient, choose a new IC with a higher current limit or increase the inductor value to reduce ΔIL.
Maximum Switch Current
The maximum switch current can be calculated as:
Isw(max) = ΔIL / 2 + Iout(max) / (1 - D)Inductor Selection
For inductors:
L = Vin × (Vout - Vin) / (ΔIL × f × Vout)Choose an inductor with a current rating higher than Isw(max).
Inductor Ripple Current Approximation
Approximate the ripple current as 20% to 40% of Iout(max):
ΔIL = (0.2 to 0.4) × Iout(max) × Vout / VinRectifier Diode Selection
For the rectifier diode, use:
If = Iout(max)The diode’s power dissipation can be calculated as:
Pd = If × VfWhere:
- If = average forward current of the diode
- Vf = forward voltage of the diode
Schottky diodes are recommended due to their low forward voltage drop and high peak current rating.
Output Voltage Setting
Most converters set the output voltage using a resistive divider network (this may be built-in for fixed output voltage converters).
With the given feedback voltage Vf and feedback bias current Ifb, the voltage divider can be calculated. The current through the resistive divider should ideally be about 100 times the feedback bias current:
Ir1_2 >= 100 * Ifb ---------- (9)Where:
- Ir1_2 is the current through the resistive divider to GND.
- Ifb is the feedback bias current from the datasheet.
This ensures less than 1% inaccuracy in the voltage measurement. However, lower resistor values can increase power loss in the resistive divider, which may be unsuitable for high-efficiency designs.
With the above condition, the resistors can be calculated as follows:
R2 = Vf / Ir1_2 ---------- (10)
R1 = R2 * [(Vout / Vf) - 1] ---------- (11)Where:
- R1 and R2 are the resistive divider resistors.
- Vf is the feedback voltage from the datasheet.
- Ir1_2 is the current through the resistive divider to GND, as calculated in Equation 9.
- Vout is the desired output voltage.
Input Capacitor Selection
The minimum value for the input capacitor is typically specified in the datasheet. This value is crucial for stabilizing the input voltage under the peak current requirements of a switching power supply.
Low ESR ceramic capacitors are preferred, and the dielectric material should be X5R or better. This avoids significant capacitance reduction due to DC bias or temperature effects.
If the input voltage is noisy, the capacitance value may need to be increased.
Output Capacitor Selection
To reduce output voltage ripple, small ESR capacitors are ideal. Ceramic capacitors with an X5R dielectric or better are recommended.
For converters with external compensation, any capacitor value above the minimum specified in the datasheet can be used.
However, the compensation must be adjusted accordingly. For internally compensated converters, the recommended inductor and capacitor values should be followed, or the datasheet guidelines should be used.
For secondary compensation, the following equations can help adjust output capacitor values for a desired output voltage ripple:
Cout_min = Iout_max * D / (fs * ΔVout) ---------- (12)Where:
- Cout_min is the minimum output capacitance.
- Iout_max is the maximum output current of the application.
- D is the duty cycle calculated using Equation 1.
- fs is the minimum switching frequency of the converter.
- ΔVout is the desired output voltage ripple.
The ESR of the output capacitor introduces additional ripple, calculated as:
ΔVout_ESR = ESR * [(Iout_max / (1 - D)) + (ΔIL / 2)] ---------- (13)Where:
- ΔVout_ESR is the additional output voltage ripple caused by the capacitor's ESR.
- ESR is the equivalent series resistance of the output capacitor.
- Iout_max is the maximum output current of the application.
- D is the duty cycle from Equation 1.
- ΔIL is the inductor ripple current from Equation 2 or Equation 6.
Important Equations for Boost Converter Power Stage
Maximum Duty Cycle:
D = 1 - (Vin_min * n / Vout) ---------- (14)Where:
- Vin_min is the minimum input voltage.
- Vout is the desired output voltage.
- n is the efficiency of the converter (e.g., 85%).
Inductor Ripple Current:
ΔIL = Vin_min * D / (fs * L) ---------- (15)Where:
- Vin_min is the minimum input voltage.
- D is the duty cycle from Equation 14.
- fs is the nominal switching frequency of the converter.
- L is the chosen inductor value.
Maximum Output Current of the Selected IC:
Iout_max = [Ilim_min - ΔIL] * (1 - D) ---------- (16)Where:
- Ilim_min is the minimum current limit of the integrated switch (from the datasheet).
- ΔIL is the inductor ripple current from Equation 15.
- D is the duty cycle from Equation 14.
Application-Specific Maximum Switch Current:
Isw_max = (ΔIL / 2) + (Iout_max / (1 - D)) ---------- (17)Where:
- ΔIL is the inductor ripple current from Equation 15.
- Iout_max is the maximum output current of the application.
- D is the duty cycle from Equation 14.
Inductor Calculation:
L = Vin * (Vout - Vin) / (ΔIL * fs * Vout) ---------- (18)Where:
- Vin is the nominal input voltage.
- Vout is the desired output voltage.
- fs is the minimum switching frequency of the converter.
- ΔIL is the estimated inductor ripple current (see Equation 19).
Inductor Ripple Current Estimation:
ΔIL = (0.2 to 0.4) * Iout_max * (Vout / Vin) ---------- (19)Where:
- ΔIL is the estimated inductor ripple current.
- Iout_max is the maximum output current required.
Rectifier Diode Parameters:
- Forward Current:
If = Iout_max ---------- (20)- Power Dissipation:
Pd = If * Vf ---------- (21)Where:
- If is the average forward current of the rectifier diode.
- Vf is the forward voltage of the rectifier diode.
Resistive Divider Network:
- Current:
Ir1_2 >= 100 * Ifb ---------- (22)- Resistor R2:
R2 = Vf / Ir1_2 ---------- (23)- Resistor R1:
R1 = R2 * [(Vout / Vf) - 1] ---------- (24)Output Capacitance:
Cout_min = Iout_max * D / (fs * ΔVout) ---------- (25)Ripple Due to ESR:
ΔVout_ESR = ESR * [(Iout_max / (1 - D)) + (ΔIL / 2)] ---------- (26)These equation provide a comprehensive guide for designing and analyzing the power stage of a boost converter.
I am trying to make 2 similar circuits that can take 2 AA batteries and output 9, and 18V DC, would this process work for making those circuits or do you have other suggestions.
1 circuit needs to take 3V in and output 18V DC, the other needs to output 9V DC
For your application a joule thief circuit might be more suitable:
https://www.homemade-circuits.com/1-watt-led-driver-using-joule-thief/
Hello sir, hope you’re doing well
Pls how can I trigger a MOSFET IRFZ44N with BJT since my pulse voltage is 5v and the vgs(gate voltage of the MOSFET is 10v)to trigger it appropriately ?
Hello Akafac,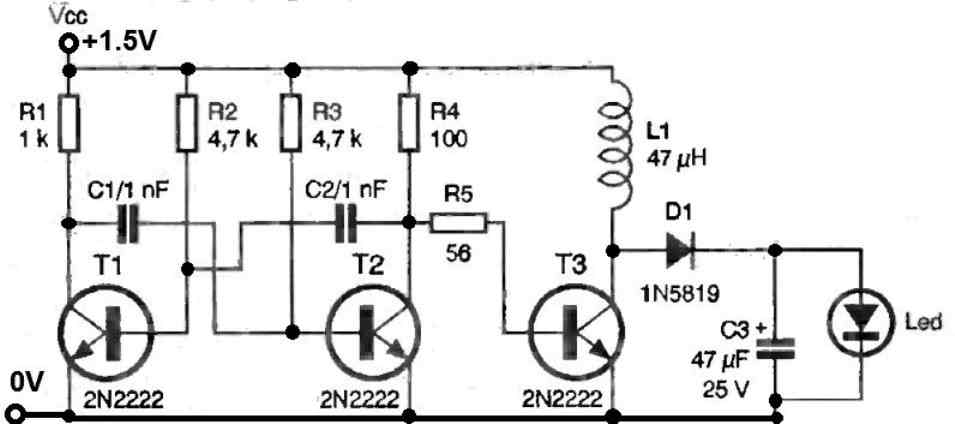
If you are having a separate 10V DC then you will need two BC547 to amplify and invert the 5V to 10V.
If you do not have a separate 10V then you may need a boost converter circuit.
" rel="ugc">
Greatings sir pls on your 1st diagram simple smps boost converter I tried to run the simulation but my proteous display 2 error sms
1 was stating no specification for D1 (FR107)
2nd pls is the zener operating ?
Hi Akafac,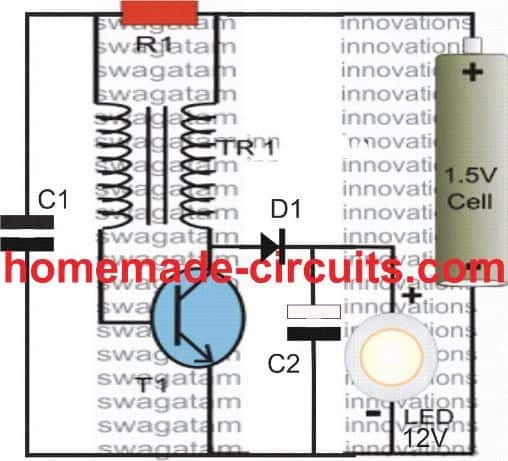
It is difficult to tell why the simulation is showing the error.
You can try the following design instead and let me know how it goes:
" rel="ugc">
Pls sir for the above circuit I’ll need the specifications of TR1 on the diagram
For the exact specifications you can refer to the following diagram: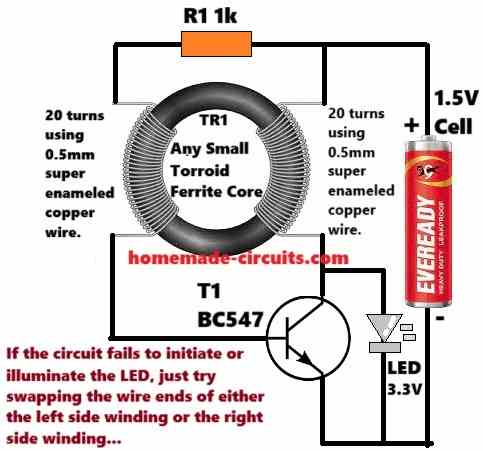
" rel="ugc">
For the transistor, please use a TIP122, for handling 1 amp current.
Thanks very much sir pls I have seen and article online on this topic I want to share with you but your email isn’t reachable I have simulated it it’s almost on point but pls I need some guidance sir
Pls can you send me your email to my Gmail so that I forward to you the link to it sir ? Thanks
Akafac, unfortunately I do not work with simulators, instead I use my knowledge based brain simulation and finally by testing through practical experimentation. I have tested the above circuit and it works wonderfully well.
If you any other questions regarding the circuit working, please let me know, i will try to help.
Greatings sir, pls my 5v to 12v boost converter I couldn’t calculate the inductor value and filtering capacitor value that will give me a constant 12v out I intend to take in 5v , send out 12v , out put current of 2A taking in to consideration a feedback system but my switch should be trigger by a pulse sign maybe generated by NE555 which is supply by a 5v dc in put which oscillate to generate the pwm to drive my switching regulator
Pls sir I need your total help again
My specifications are
1 input 5v , output 12v , output current 2A,
Thank
Hello Akafac, here are the calculations for your application:
Specifications:
Input Voltage = 5V
Output Voltage = 12V
Load Current = 2 Amps
Duty Cycle Calculation:
D = 1 – (Vin / Vout)
D = 1 – (5 / 12)
D = 0.5833 (58.33%)
Output Power:
Pout = Vout * Iout
= 12 * 2
Pout = 24W
Input Current:
Assume efficiency (η) = 80% = 0.8
Iin = Pout / (Vin * η)
= 24 / (5 * 0.8)
= 24 / 4
Iin = 6A
Inductor Value:
L = (Vin * D) / (f * ΔIL)
Where ΔIL = Ripple Current = 20% of Iin = 0.2 * 6 = 1.2A
Assume switching frequency (f) = 50kHz = 50,000 Hz
L = (5 * 0.5833) / (50,000 * 1.2)
L = 2.9167 / 60,000
L = 48.61 µH
Choose standard value: 47 µH
Output Capacitor Value:
Cout = (Iout * D) / (f * ΔVout)
Where ΔVout = Output Ripple Voltage = 0.1V
Cout = (2 * 0.5833) / (50,000 * 0.1)
Cout = 1.1667 / 5,000
Cout = 233.33 µF
Choose standard value: 220 µF or use parallel capacitors.
Resistor Values for IC 555:
Frequency formula: f = 1.44 / ((R1 + 2R2) * Ct)
Assume Ct = 10 nF = 0.00000001 F
R1 + 2R2 = 1.44 / (f * Ct)
R1 + 2R2 = 1.44 / (50,000 * 0.00000001)
R1 + 2R2 = 1.44 / 0.0005
R1 + 2R2 = 2880 Ω
Choose R1 = 1 kΩ = 1000 Ω
2R2 = 2880 – 1000
2R2 = 1880 Ω
R2 = 1880 / 2
R2 = 940 Ω
Sir, thank very much God blessed you for your good works indeed I acknowledge your kind heart
You are most welcome Akafac.
Greatings sir pls when calculating the capacitor value why did you assume ripple voltage of 1v, and for the inductor you assume o.4
Hello Akafac,
we must assume Ripple Current as a Percentage of Load Current if Input Current is Not Clearly specified.
If input current Iin cannot be estimated and an “optimal” ripple current is assumed, use a rule-of-thumb based on the load current (Iout):
Typical Design: Assume Δ I = 20-30% of Iout.
High-Efficiency Design: Assume Δ I = 10-15% of Iout.
Example:
For Iout = 2A:
Δ I = 0.2 * 2 = 0.4A (20%).
Δ I = 0.1 * 2 = 0.2A (10%)
Fine boosted sir but the out put voltage is not stable it’s increasing from 12v to 15v
Akafac, did you build it practically, or doing a simulation? because I cannot help with simulations, I can only help with practical working.
Try increasing the output capacitor value and check again.
Thanks very much sir, the PWM oscillator circuit with NE555 is working ok for 50khz, 58.33%
Pls I wish to add a feedback circuit to it pls how do I go about it?
Thanks Akafac, the feedback circuit is given at the end of the post.
Good day sir hope you’re doing well, pls my teacher ask me to used ATMEGA 32 to generate to PWM
Instead of NE555 pls help sir
Thanks
Sorry Akafac, my microcontroller programming knowledge is not good, so I may not be able to help you in this regard….
Thank you sir I applaud
You’re a kind person
Thank you Akafac, for your kind words, I appreciate it. I Hope you find someone who can do it for you…
Yes sir it’s working well but the diagram you gave me and the calculations are perfect I’m fine now my circuit is ok thanks sir
Thanks Akafac, Glad to know it is working. All the Best to you…
Hello sir, please I saw a 12v , 8A to 24v, 8A converter,
1. is this boost or buck converter because it increases the power?
2. please help Me with a circuit for it?
3. please how can I use such converter for infinity power supply?
Hi Daniel,
That is a boost converter, but the output current will not be 8 amps, it will be around 3.5 amps.
Power can never be boosted, output power will be always lower than the input power.
Thanks sir, engineer Swagatam, you are correct, it was typo error on the converter presentation.
No problem Daniel, glad it helped!
I have tried but very tedious by trial and error. Thanks for always.
please I will know the appropriate frequency and inductor for a particular design.
You will have to adjust it with some experimentation, and trial and error. I can help you with this…
Hello sir, thanks for your informative response. I want to do a 555 boost converter with a feedback loop, someone recommended that for a 36v-48v I will need a zener diode in the feedback line, I don’t know the reason and where I will put it.
please kindly guide. thanks sir, Engineer Swagatam
Thank you Daniel,
Yes you will need a feedback loop to be connected between the output and the shutdown pin of the control IC.
Please see the last diagram in which you can see the feedback is connected with the pin#5 of the IC555.
The feedback loop makes sure that the output voltage remains fixed as set by the feedback level.
please how will I set the feedback to appropriate level.’?
Please build the basic 555 boost converter design first then I will tell you how to set the feedback…
I have built 555 ic converter as specified in the article but I am not getting the feedback, please guide, sir.
Daniel, Try the following circuit, and use 100 turns for the coil over a ferrite rod.
Make sure to connect a 1n4007 diode across the collector/emitter terminals of the transistor.
" rel="ugc">
Check the output voltage, it must much higher than the supply input DC.
First confirm this, then we can go for the feedback.
Thanks sir, fine boosted the voltage from 12.5v to 22.7v, but not stable. please what next, sir?
Daniel, now you can add the feedback as shown in the following circuit:
" rel="ugc">
Please replace the 10k preset with a 100k preset, and replace the resistor between pin#7 and positive with a 10k, and remove the 10k connected parallel to the output capacitor, it is not required.
How do make the output stable
If you put overload at the output, then the feedback will not work….and output voltage will drop..
please if I want to boost to 96v from 12v, how many turns to use and wire. guage. thanks sir.
That will need some experimentation, but it is not difficult, just go on increasing the number of turns and also tweak the PWM/frequency of the 555 until you get the optimal outcome…
Sirji, thanx for quick reply. Just for reminder, I’m already working on the car laptop charger ckt. I asked for the ways for making this adjustable! Please suggest some ways that can vary the output voltage without modifying the turns of the inductor!
Maddy, you can modify it in the following manner to get an adjustable boosted output.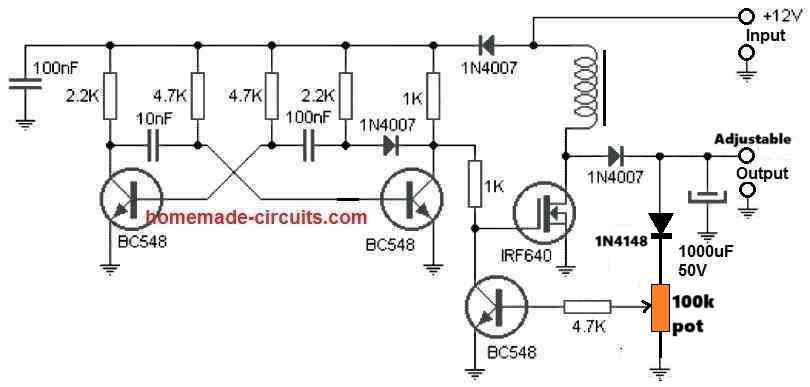
" rel="ugc">
Sirji I have a small question! Most of the commercially available booster ckts have variable output facility with them. Can we have any modifications for our booster ckt have this freedom! Say by adding a pot at any stage to vary the output. This wud make it more versatile! Thanx in advance!!
Maddy, the 555 IC boost converter is adjustable using the feedback pot.
The following designs are also adjustable:
https://www.homemade-circuits.com/high-power-dc-to-dc-converter-circuit-12-v-to-30-v-variable/
https://www.homemade-circuits.com/12v-car-laptop-charger-circuit-using/
Sirji! Thnx for the advise! But I’ve used some wrong terms here! Actually I was asking for the disturbance due to the magnetic field of the inductor to the Audio content being amplified in RF range! Presently the ckt is perfectly working with 19v adapter! But I was intending to raise the supply up to 24v. Searching the net I came across various methods said before. So I asked for your expert advise!! Thanx again!
Thanks Maddy, glad to know " rel="ugc">the circuit is working for you.
Yes, in that case it is better to encapsulate the ferrite inductor inside a Mu-metal enclosure.
Let me know how it goes.
Sirji, I finally got my ferrite core at a decent price from a radio technician. Before putting everything to PCB, I’ve a final hurdle to remove! I wud be using this booster to power a small RF amplifier ckt. So the question is, should I shield above inductor inside some Mu-metal or steel type enclosure to prevent the noise from this booster from disturbing my RF amplifier ckt? Or the simplest method to do this is to keep both ckts far away from each other. Or another way is just to keep the inductor away! And if this is done, is there any effect over the output voltage? Please advise!! Thanx again!!
Maddy, Referring to the following booster converter circuit, this is suitable for high power loads, if your load is a small RF amplifier then this circuit may be an overkill: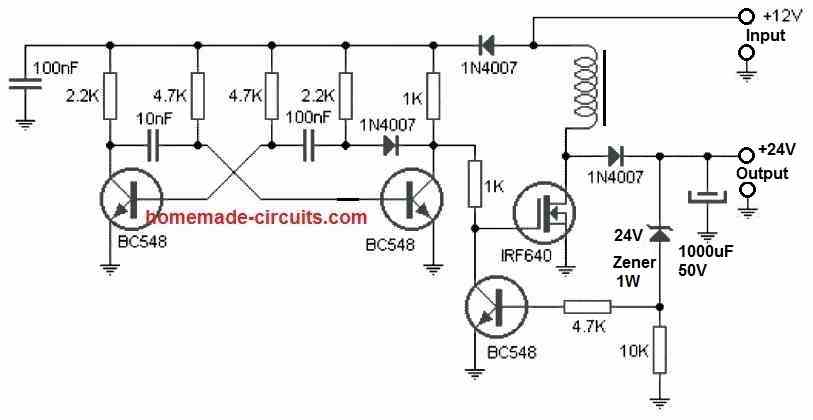
" rel="ugc">
Regarding the RF noise, it can be eliminated by using an large filter capacitor across the supply terminals of your RF amplifier, in addition to the one which is already included at the boost converter circuit output.
Let me know if you have any further doubts.
Sir just to get a ferrite core, I’ve extracted a torroidal ceramic magnet from small speaker. having 2″ external and 1″ internal dia. I could not find any other solution over the Internet for 3″ long, 1cm dia ferrite rod. The available ones were very small in size. Now I’m planning to demagnetize above torroid using AC current using shielded wires. I don’t know how long it wud take. But in the mean time, if you do know of any such cheap rod being sold online, please give me the link! Thanx again, Sirji !!
Hello Maddy,
the ferrite rod size is not critical at all, you can choose any standard ferrite rod, or even a standard ferrite ring can be used.
I don’t think a magnet can be converted into an inductive core by demagnetizing it.
All components gathered!! Except Ferrite core. I searched but ended with whooping prices!! Sir can I prepare a core using Powdered Iron as seen over the Internet!! Just using the term “DIY Ferrite core alternatives” gives you different sites that show you how one can make one using cheaper materials. What opinion do you have about this? Or the same cmt be made using Air core too?
Thanks Maddy,
Referring to the following diagram:
" rel="ugc">
Ferrite core will make the inductor a lot smaller and compact, whereas the same inductor can be quite bulky if an iron core is used and also for an iron core the frequency will need to be drastically reduced.
I don’t think there’s any cheaper alternative to ferrite cores, so it is not possible find any suitable alternative.
Air core is possible which will be even bigger in size than an iron core inductor.
If you are sure you can make a proper iron powder core, you can try it, but then the winding might need to be increased 5 times more and the frequency reduced proportionately.
The frequency can be reduced by increasing the base capacitors of the BC548 transistors.
Sir thank you for your quick response! I’ve a bit of problem here! As per your advise, the circuit should have a IRF640 but can I use IRF3205 there?
Hi Maddy, no issues, you can use any appropriate MOSFET whose voltage and current ratings are higher than the input/output ratings of the circuit.
So, an IRFF3205 would be perfectly fine here.
Sir, I have a 19V, 2.1A Laptop adapter! Please suggest me any boost converter circuit that can be made using locally available cheap components to up-convert above DC supply to 24V, atleast 1A DC! For one week or so, I have become a fan of your site. The more I dive into different articles, the more curious I become about the extent of knowledge still on your site but hidden from my eyes.
Thank you so much Maddy, I am glad you found the site helpful.
I think you should try the first circuit design from the following article:
https://www.homemade-circuits.com/12v-car-laptop-charger-circuit-using/
You will have to experiment a little with the coil to get the perfect desired results.
Let me know if you have any problems.
I’ve been following your educative posts and used most of them on my projects successfully. I thank you for that most sincerely. Currently, my question is; I want to boost 48v from a SMPS to 54v to charge two 48v 100AH connected in parallel ie these are EMS intelligent batteries. I need a schematic diagram.preferebly and possibly if this converter out put can be variable.Thanking you in advance.
Thank you for your kind feedback, glad I could be helpful.
I think you can try the first circuit from the following article, however this circuit will need to be experimented and modified appropriately as per the 48V input and 54V output.
The output can be made variable by removing the zener diode and the 10k, and replacing them with a potentiometer instead.
https://www.homemade-circuits.com/12v-car-laptop-charger-circuit-using/
can i put a coil of copper wire instead of an inductor
Yes copper coil will do but the inductance has to be matched correctly
What will I change in the circuit if I replace the Bc557 with A1015 bjt
You can try it, no changes will be required.
Good day sir,
Please can you help me on how to build 5V 2AMP, step up converter that works on voltage from 3v to 4.2v.
Using 50, or 100khz transistor oscillator.
I have a 5,000mah li-lon battery to power it
Hi Chidonlite,
I think you should try the first circuit from the above article. You can tweak and adjust the 12V zener diode to get the desired voltage at the output. For 2 amp current, the 2N2222 can be replaced with a TIP31 and the BC557 with a 2N2907…
Hi @Swagatam. I really need your help with a boost converter circuit that I can use in my car to power up my laptop. The laptop takes in 18.5vdc at 3.5amps. thanks
Hi Breno1, You can try the following design. The inductor can be built by winding 25 or 30 turns using 1 mm super enameled copper wire over a ferrite core. The ferrite core can be a ferrite rod or a ferrite ring. The 24V zener can be replaced with a 20 V zener diode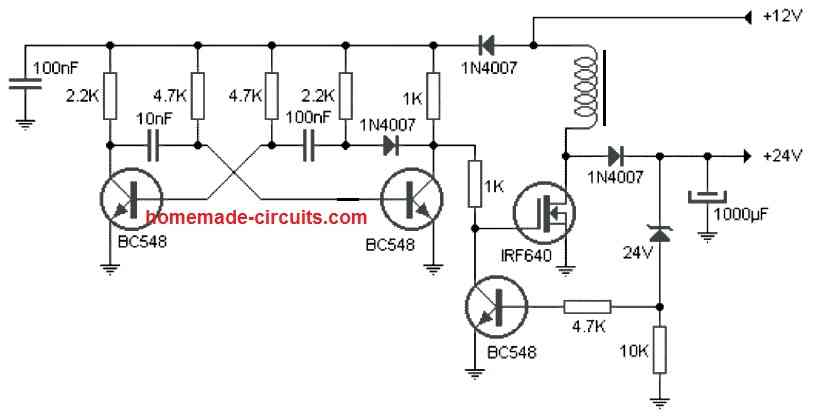
" rel="ugc">
Thanks a lot for the circuit @Swagatam.
1. I have two inductors each has 15 turns, will it work if I connect them in series to get 30?
2. About the capacitors. Am I to us same type i.e polarized electrolytic capacitors?
@Breno1,
1) No two series coils will not work, you must build the coil over a single ferrite core
2) The nF capacitors can be disc ceramic type, uF capacitor can be an electrolytic.
Please I need circuit diagram for 12vdc to 400vdc converter
You can try the following design:
https://www.homemade-circuits.com/how-to-convert-12v-dc-to-220v-ac-using/
For the flyback circuit could I use 5v input instead of 1.5v?
You can use 5V, but then the output would be above 24V
That is what I need, thank you
You are welcome! Glad you found the post helpful.
Hi sir, thanx for wonderful circuits and your knowledge to, am my question is what if I use tip41c instead of BC 547 will the circuit function properly?
Thank you Nedi,
I don’t think TIP41C would work correctly instead of BC547, because BC547 has high gain and requires very little current to switch ON, while TIP41 might need a lot more current to switch ON. This might need modifications for the base resistors of the transistor.
Hi, what could you suggest I use to boost a dc 2.0 volt RSSI (relative signal strength indicator) voltage up to about 5 dc volts so I can run a bar graph module. This to show how much RF signal my radio is getting.
Hi, you can try the second or the third circuit from the above article, it should work for your application.
Sir, I thought the minimum supply voltage for lm555 is 4.5v, how then is it able to boost 3.7 lion battery to 24volts. Is it really possible that way.
Moses, you can use the CMOS 7555 IC which are rated to work from 3 V onward.
Yes I have recently made did experiment .by using mje 13003 transistor and 10k resistor and capacitor 35 volt 2200 uf. And the input is 3.7 while the output replect about 28 volt DC.but de battery did not last at all
sir i want to know if it is possible to connect phone batteries together either in series or parallel. If it is possible i have a plan to connect four of them in parallel each of 2500mAH. But i want you to help me with a circuit that can be able to charge it automatically
Hi Alimon,
You can connect the batteries in parallel. However making an automatic charger can be difficult for a newcomer, therefore I would suggest using a high current LM317 based power supply and adjust its output to exactly 4.1 v so that over charging of the battery can be avoided.
4 batts in parallel would mean a total Ah rating of 10 Ah which will require a charging current of 5 amp. You can use a 9V 5 amp transformer to build the voltage/current source for the LM317 circuit.
You can try the following circuit for the mentioned purpose. Use only 2nos of 2N3055 in the circuit, that will be enough:
" rel="ugc">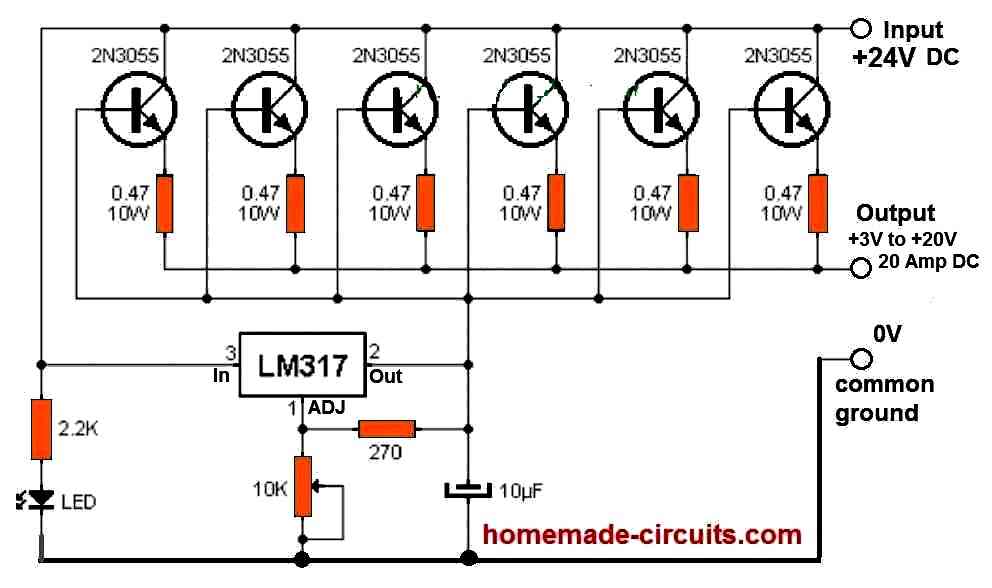
These circuits look nice, and the principle is explained well.
Is there any circuits that can boost low voltages?
From as low as 30mV to 5V, other than using an LTC3108.
Or from 0.8V to 5V
Yes boosting 0.8V can be possible through a joule thief circuit. You can try the first circuit explained in the following article:
3 Best Joule Thief Circuits
Thank you, I don’t really understand why, but I’m looking through the article.
Is it possible to boost from as low as 0.1V. without using a 1:100 current transformer (cause that’s not available in my region)
Without a transformer that can be impossible. Moreover I think 0.4V is the last limit which can be boosted using a joule thief circuit….0.1 is too low for boosting
Hello there can i use a peice of ferrite rod instead of a ferrite toroide.
yes you can do that!
Cheers mate that will save me from having to wait a week for delivery of toroid core.
Sure, no problem, and wish you all the best!
Please email me via [email protected] so i can share a circuit photo with you, and,
happy Fathers’ Day, Professor Swagatam !
Thank you Doctor B, My email is homemadecircuits @ gmail . com
hello sir,
sir, if i use the first circuit “Simple Boost Converter using a single BJT” with 3.7volt input is there any component values that need to be replaced?
is this circuit efficient for long time use?
Hello Ningrat, for 3.7V you don’t have to change any components in the first diagram, however the BJT specs actually depends on the load specs.
Yes the circuit is efficient for a long term use.
Hello good afternoon, what is the output amperage of the circuit with Lm555 ..
It is 1 amp because TIP31 is used, you can try TIP35 for higher amps
Swagatam, in your article on boost converters, specifically diagram “3.7 to 24V converter”, there is a 10K resistor on the output side. I can’t figure out what its purpose is. It appears that it would bleed energy from the output capacitor. What is its purpose?
Also, when does the diode conduct? It appears it conducts when T1 is off. When T1 is on the coil conducts, right? Please explain a little more where the “boost” comes from.
Thank you, regards, Cris
Cris, yes the 10k is the bleeder resistor, and will act like a load when no real load is connected.
When the transistor is ON, the coil keeps storing the charge until it has reached its peak voltage specification. Then when the transistor switches OFF, this stored peak voltage is fired back as a boosted voltage.
The peak voltage depends on the number of turns, higher turns will generate higher voltage, and proportionately lower current.
hello im interested in making a earth battery im asking can i use a joule thief to take the volts form 0.5 to 12 volts and how to get more amps
Hi, Either you get amps, or volts, you can never get them together for free…
for an earth battery you may have to integrate huge number of plates in series parallel to get a decent power output
Glad to find this article, Well done Swagatam.
Please I want a boost converter design in which I will use 100w/12v panel to charge 4*18ah/12v 48v system.
Thanks
Thank you Seun, I think the following design will be more suitable for your application:
https://www.homemade-circuits.com/high-power-dc-to-dc-converter-circuit-12-v-to-30-v-variable/
Mr. Swagatam
I like your “simple boost circuit. I appreciate your response, the 12 v laptop charger circuit, I’ll study it. I find now that we need to get up to approx. 200 volts output from 9 volts input. I still need a bit of couching. Thanks again. Vernon
You are welcome Mr. Vernon!
For higher voltages you can using a small 9-0-9V 220V 100mA transformer, and use it in place of the inductor shown in the IC 555 circuit. This is hopefully help to accomplish the required results quickly!
Good morning
Working on a project that includes “boosting” 9v DC (battery) to 50 to 100v DC.
We’re not sure of the circuit design or components. We want it to be able to recharge for follow on use. (all going in a small package).
Have you done such a project that you could permit us to reference?
We appreciate the assistance.
Hello, you can try the first concept presented in the following article:
https://www.homemade-circuits.com/12v-car-laptop-charger-circuit-using/
Mr Swagatam, I was still wrong in wrapping the enameled wire on the toroid, could you give an example in the form of a picture, but not a symbol
Mr.Rudi, the winding is not critical at all. Just wind the two sides anyway you want, and after connecting it to the circuit if the circuit doesn’t work, just interchange the wire ends of any one of the winding, and your circuit will start working instantly.
Good evening sir,pls I we like to learn more on dis DC 1.5 converter to DC 12 voit
Good day sir please for the first diagram I can’t really find a 1000uf capacitor and also the 0.0045uf
So can I try using 220uf and 22uf
Ordu, 1000uF can be replaced with 220uF, but the 0.0047uF value cannot be altered, you can adjust the value through series parallel capacitors if required.
Please is there any other pwm oscillator ic I can use instead of 555 or can I equally use the popular viper22A or Rm6203 used for flyback converters, will it work.
You can use TL494 IC or similar, but VIPER can be difficult since it is configured to work with high voltage rectified AC.
Ok I’ve just made the circuit, and am continuously having this problem of magnetostriction. According to my research, I find out that it is due to low frequency switching. So please can you tell me how I increase the switching frequency, and also the factors and components value that affect the frequency of operation.
If you are referring to TL494 circuit, you can change its Rt, or Ct values to change its frequency.
No it’s the first version of the joule thief circuit.
Did you confirm the frequency with an oscilloscope? Since it’s a self oscillatory type circuit frequency is pretty much fixed. For higher frequency you can probably try the following version:
8X Overunity from Joule Thief – Proven Design
Dear sir Swag, truly you have swag! I have been looking for this information for years but thanks to you I found it! Also, can the resistor be added after the toroidal core? Like directly at the base of the transistor?
Thank you Miracletech, yes you can try that for the first diagram. For more options you can also refer to this article:
https://www.homemade-circuits.com/1-watt-led-driver-using-joule-thief/
Ok. Thank you so much.
can we use this circuit(555) to boost voltage from solar panel (12v to 15v)?
yes, it is possible.
Dear Swag,
I do have a 12volt @75 amp dc battery and do intend to use to power about five led corn light bulbs and rating for each is 359 milliamps and wattage for each is 26 watts. I will be using the constant current method to drive the led driver to power the lead lights. The led driver can be a buck boost converter, sepic dc dc converter or cuk dc dc converter. The problem I am having is that of stepping down the high dc current from 75 amps to manageable one like say 13 amps. If it were ac it would be easier. What I am requesting from you is a general method which I can apply.
Dear Bernard, what is the voltage spec of the LED, there’s no need of a buck boost circuit, you can directly use the supply for the LEDs after configuring the LEDs appropriately.
Good evening sir,
very difficult to leave your pages. Your information is always precious.
Transistors in Darligton mode would lift me the current in these joule thief if powered by solar cell?
If not, is there any other way to get a current gain?
If it were a buck converter would there be a way to take advantage of the current of the dissipated voltage?
Thank you very much in advance.
A lot of Swag light
Thank you Marcelo, appreciate your interest very much!
A Darlington may help to increase the current transfer response. However, using many thin wires together for the winding may also help to gain more power from the design. A joule will normally work like a boost converter so not sure how it may be turned into a buck converter…but I don’t think this concept can be used effectively used for charging bigger batteries.
Hello sir
For giving the gate pulse to the BJt can i give it through Arduino?
like pwm technique
Hi Parsiva, you can do that, just make sure that the duty cycle and the frequency are optimally adjusted.
Goodday sir I really want to appreciate you for good work thank you very much please keep up
Sir please I build a boost converter using 555 timer to drive my mosfet, and I use a mosfet in place of the transistor but each time I power it up the mosfet get really hot please what could be the cause I have checked but can find any fault in the circuit
Hello faith, keep the frequency at around 50 kHz, and test by gradually increasing the turns until the MOSFET stops heating, this is perhaps the easiest trial and error way to optimize a boost converter.
Which turns is it the number of turns i.e the inductor
There’s only one component in 555 circuit which has turns, it’s L1
Sir I have seen my mistake all this while the diode was connected wrongly but now is working very well thanks for your assistance
Glad you could solve it!
Sir I did exactly what you said it still the same I noticed that when ever I connect the power supply it like both positive and negative are connected together it al hiways spark and if I try leave it for some second the wire Wil burnt out but if i remove the inductor it will not happen, and the output power is not boost please what could be the cause. The inductor I’m using is wound on a toroid core
How many turns did you use? and what at what frequency did you set your IC 555?
Sir I’m really confused here, I even try building the boost without the 555, i.e the simple circuit were I have just inductor, diode pull button switch and capacitor, when ever I pushed the switch the inductor Wil connect it to ground i.e shorting the circuit why this happening
The switching should be in millisconds, if you hold it even for 0.25 seconds it will create a short circuit. You can read the following article for more info:
https://www.homemade-circuits.com/how-boost-converters-works/
sir I made this circuit but its not working I can’t find 680pf but am using 2A682k then I cant get tip31 and am using tip41 while testing it its just sparking as if I shot the circuit of the battery then the transistor is getting hot please help me
damilare, 2A682k = 6800pf, it’s not 680pF
In your present set up increasing the number of turns to 5 times more than the shown value, and check the results. Wind it on a ferrite rod.
adofo I have 5v 500ma solar panel. can I use your booster convert to run car tape
5 x 0.5 = 2.5 watts that’s too less for a car tape, it won’t work
Hello,
Sir can i use N-channel mosfet instead of transistor? for T1 & BC547?
is there any modifications for this?
Thanks a lot..
Hello Paul, mosfets will require minimum 9V to turn ON fully, so it cannot be in these applications.
Thanks for the reply then can i use 13003 transistor for T1?
I am sorry Paul, for BC547 you can use a mosfet since the gate would be receiving a boosted 12V so no problem.. MJE13003 won’t be suitable here!
I cant find any TIP31 Its hard to find here in our place but i found TIP41 & TIP42, can it be used here in the circuit ?
Thanks…
TIP41 is fine, it will work…
Sir Can I use 100nf cap instead of 680 pf? i cant find that capacitor.. and 1n4007 diode instead of FR107.
thanks again..
Hi Paul, There’s a huge difference between 100nF and 680pF, so it won’t work. You can try the first circuit instead.
Hmm, if Paul been asking about replacing T1 BJT with 13003 it would probably work, since 1300x family is just (high-voltage) NPN BJTs, not anyhow worse than any others. They are pretty typical in CCFLs and dumbest “electronic transformers”, esp these for “halogen lamps” and even some cheap SMPS designs.
It will work but with poor efficiency, that’s the reason we have such a huge range of devices designed for different voltage or current specs, otherwise the manufactures could have designed a single all purpose 1kv transistor : )
Yes, but if one goes for joule thief or 555-driven circuit, especially with BJT as switch and FR107 as diode, they don’t have to expect superb efficiency or awesome output power in compact package, right?
This said, joule thief is funny thing to power small led or so out of 1.5 volt battery. Only few relatively exotic and expensive DC-DC ICs would start up from voltages that make “joule thief” happy.
Actually a joule thief circuit is supposed to be extremely efficient, that’s why it’s called a “joule thief”. Yes, it’s been one of the most interesting inventions so far, considering the fact that it can work even with voltages lower then 0.5 V.
Joule thief key property that makes it interesting is that it runs down to like 0.3V or so, draining 1.5V batteries way below what most of other electronics could afford. Say, most CMOS-based ICs have a problem that 0.3V is way below of threshold voltage. Even “special” boost ICs like NCP1400 would start up from like 0.8V – then it would hold down to like 0.3V as well – because they start up, and then supply self out of own boosted output. However it implies startup problems if battery got below 0.8V and “cold” start happens.
This said, joule thief is kind of “blocking oscillator” – so it got no reasons to be terribly efficient. Waveforms aren’t really perfect, BJT drops some tenths of volt on C-E junction even if current is small, etc (FETs get edge in this regard generally, but most MOSFETs got threshold over 1V, so running less than 1V is a problem, lowest I know have Vg_th=0.8V). However joule thief gets its edge over many other circuits when it comes to using 1.5V batteries, draining them way more completely compared to most other circuits. So it would start and work out of batteries most equipment considers long “dead”. That’s where it gets extra power margin – partially negating its imperfections, so overall performance looks rather good.
p.s. I’ve finally got right one of these 10-year-led-blink, without getting it working I would have felt ashamed way too much – failing such a simple thing is a LOL. Grossly simplifying one (as suggested on youtube comments – just thief, cap and resistor). I’ve used 5.6uF 1206 SMD cercap, 5.1M 0805 resistor, PMBS3904 in sot 23 and hi-eff blue led – overall I’ve got shy 10uA average current while still getting very persuading bright blue flash about once in couple of seconds. I’ve also found funny enclosure for this little cheat, making it look like part of office alarm system, haha. A perfect joke for few vandal-unsafe places, granted most expensive part is battery and enclosure. And according to my computations battery would last … for hell knows how long, at 10uA average it would rather self discharge I guess. That’s probably best use of joulr thief I’ve faced to the date XD
What is the advantage to get add on a transistor BC547 feedback circuit? Please give me reply….
it is for keeping the output voltage restricted to a specified limit, and preventing any rise beyond that limit.
Thanks for yours valuable reply.Yours support in electronic science field really dedicated…god bless
.
It is my pleasure Biju!
Please for the bjt booster , how can I reduce the voltage to 7v instead of 30v as designed to charge a smart phone
sorry, you cannot use a 1.5V AAA cell to charge a smart phone.
Thanks Swag, but can 3.7v lithium battery power the 555ic. You said +5v to 12v input.
Hi Grace, yes you are right, normal 555 ICs will not work with 3.7V but the CMOS version (7)555 can be used which is rated to work with minimum 3V
Hi Swagatam! I have tested the above circuit which uses a 555 timer and the output is 38.6 volts using a 100uH through hole fixed inductor. I tried changing the pin 6 to pin 7 resistor to 10K with no change. I have 22uH, 47uH, 68uH, 100uH, 220uH, 330uH 470uH, 1MuH inductors. I tried 47uH inductor and the output voltage was 38.9v. I tried 220uH and the output voltage was about 37.8v. I tried 3v, 6v, 9v, 12v input with almost the same results. It just takes longer to reach max voltage as the supply voltage is reduced.What should I modify to get 20-24v output? I only have 20volt 1/2 watt Zener available. I looked at other posts which use a Zener to control the output voltage but they require a 1-watt Zener. Thanks!
Hi Norman, you can adjust the voltage either by changing the number of turns of the inductor or simply by adjusting the 1K value between the pin#6 and 7.
Thank you sir for replying
Hello sir Swagatam,
Thanks a lot for this post.
I would like to use the IC555 version to boost 3.7V Li ion battery to 12V. What modifications do I need to make to achieve this?
Will the output be suitable for powering circuits that have ICs in them?
Thanks Godson, you can use the same design as shown in the above article
Good afternone sir!
I would like to use this boost converter (the first picture) to lit the LED at night and
as a charger (at day) of 4.5 v cell (3×1.5 cell) .The LEd position will be also the position of cells .And on the position of the cell (on the above picture) will come a small solar panel.can you show me how to do a current limiting that can be used for both task (maybe by useing poti?).
Thankyou in advance!
Hello Shigida, I think for this low current application you could probably limit the current with a resistor in series with the battery positive or negative terminal. The resistor value could be calculated using Ohms law:
R = V/I
where V will be output voltage minus battery voltage and I will be the safe charging current of the battery. Make sure the max output is slightly lower than the battery’s full charge level.
hello, how can i make the Simple Boost Converter using a single BJT circuit work with a solar panel to charge the battery?
Hi, please see the diagram at the bottom of this article, it might be just what you are looking for
https://www.homemade-circuits.com/simplest-automatic-led-solar-light/
thanks for the reply.
however i would like to use 1 battery instead of 3 to keep the circuit as small as possible.
All the circuits referred here use a single battery. So perhaps you can try the first design from the above article
Good day Swag
I am looking for a diagram to build that can do the following. Dc booster
I got solar panels that is 53 volt and an element rated 48v resistance 7 ohm. If i connect directly it pull the panels down to 3volt.i dont want to buy a geyserwise mppt just for this.
Hi Corne, a boost converter will not solve your problem, neither is it required.
A 48V 7 ohm element would require a current of 48/7 = 6 amps. So is your 53V panel rated to provide this much current? You can check this by momentarily connecting an ammeter across the solar panel during peak sunlight.
Your element is rated at 48 x 6 = 288 watts, so you will need a 300 watt panel to ensure that the voltage does not drop too much.